6ième école EGRIN

18 juin 2018, 10:45 → 21 juin 2018, 16:15 Europe/Paris

DUBOIS

Sixième école EGRIN

VVF Le Grand Lioran, 18-21 juin 2018

 

De nos jours, la prévention de catastrophes naturelles, la gestion des ressources d'eau ou encore l'impact des écoulements sur les sols et structures sont des questions d'importance socio-économique majeure. Le développement de modèles et d'outils de simulation numérique fiables et performants est essentiel à la compréhension des ces questions. Le GdR interdisciplinaire EGRIN a pour objectif de rassembler des chercheurs autour de ces thématiques pour échanger sur les avancées récentes, déterminer les verrous scientifiques existants et renforcer les collaborations.

Les exposés commenceront le lundi 18 juin en début d'après-midi et se termineront le jeudi 21 juin à midi.

Trois mini-cours sont prévus (voir les résumés ci-dessous): 

1. Aline Lefebvre-Lepot (CMAP, Ecole Polytechnique), Des granulaires aux suspensions - prise en compte des interactions proches dans les simulations numériques.
2. Didier Bresch (LAMA, Université Savoie Mont Blanc),Formulations augmentées en mécanique des fluides.
3. Guillaume Chambon (Laboratoire de rhéométrie, IRSTEA), Fluides modèles versus fluides réels : de la difficulté à confronter expériences de laboratoire et modélisations pour les fluides complexes.

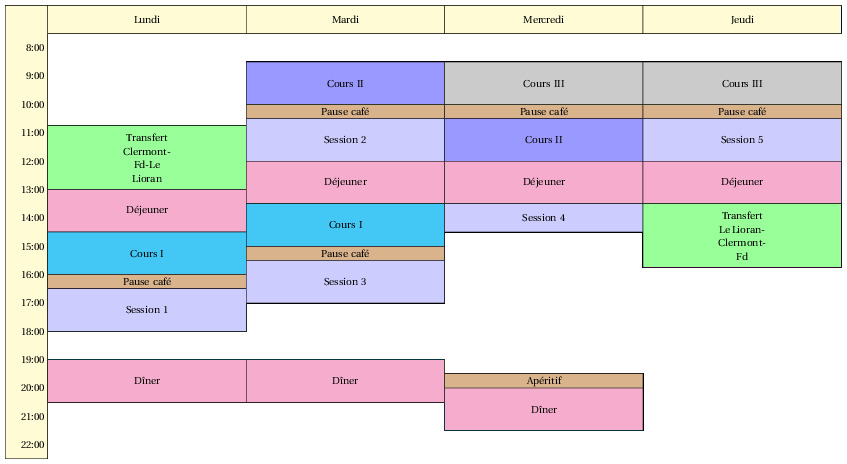
Progamme prévisionnel :

Organisation : L. Chupin, T. Dubois, C. Lucas, M.F. Grespier

Partenaires :

                                           

 

Minutes Programme_EGRIN_2018.pdf

summary Programme.pdf

lundi 18 juin

Transfert: de Clermont-Fd au VVF (Le Lioran)

13:00 Déjeuner

1 Des granulaires aux suspensions - prise en compte des interactions proches dans les simulations numériques

Orateur: Aline Lefebvre-Lepot (CNRS / CMAP-Ecole Polytechnique)

Transparents Lefebvre_EGRIN_180618-1-Contacts.pdf

16:00 Pause café

Session 1: 3 exposés de 30 mn

2 Modeling and simulation of floating objects with a congested shallow water model

We are interested in the modeling and the numerical approximation of constrained flows. Previously, a shallow water type model with a congestion constraint and its numerical resolution was proposed [1]. In order to simulate floating structures such as marine energy devices, the fluid-structure interaction of an object freely floating at the water surface is considered. The coupling with Newton's second law of motion and angular momentum theorem is explained and attention is paid to the energy of the system. The numerical approach introduced in [1] is adapted to take into account a strong coupling with the dynamics of a floating object. Furthermore the dissipation of mechanical energy is ensured. Numerical results are shown in a one dimensional framework. [1] Edwige Godlewski, Martin Parisot, Jacques Sainte-Marie, and Fabien Wahl. Congested shallow water type model : roof modelling in free surface flow. submitted.

Orateur: Fabien Wahl (LJLL (Sorbonne Université))

Transparents wahl.pdf

3 Modèles “shallow-water” pour la modélisation des mouvements gravitaires secs et hydro-gravitaires.

La propagation des mouvements gravitaires est communément modélisée par des équations de type Saint-Venant, où l’écoulement est supposé homogène et de faible épaisseur. Des rhéologies différentes tentent de rendre compte de la variabilité des processus physiques qui contrôlent la dynamique des écoulements. En particulier, le degré de saturation en eau impacte fortement le comportement visqueux du fluide. Nous nous intéressons dans un premier temps aux écoulements granulaires secs, pour lesquels l’interaction avec la topographie est assez bien décrite par des lois de friction solide. L’expression des forces exercées à la base de l’écoulement comprend alors un terme de courbure qui impacte fortement la dynamique de l’écoulement. Des comparaisons ont été réalisées avec le code SHALTOP qui a reproduit avec succès des écoulements granulaires en laboratoire et des mouvements gravitaires sur le terrain. Nous utilisons des topographies synthétiques en considérant deux situations : (1) quand la courbure dans le sens de l’écoulement est approximée, et (2) quand le tenseur complet de courbure est pris en compte. Sur des topographies reproduisant des chenaux avec des changements de direction, les phases d’accélération et de décélration sont significativement différentes. L’ordre de grandeur des différences observées est par ailleurs comparable aux différences entre les résultats de SHALTOP et VOLCFLOW, un autre code communément utilisé. La modélisation d’écoulements dont le degré de saturation en eau n’est pas négligeable est plus complexe : les rhéologies de friction solide ne permettent pas de reproduire la dynamique d’écoulements visqueux et visco-élastiques. D’autres rhéologies, comme celle de Bingham, on été introduites pour remédier à ce problème. Le travail en cours vise ainsi à intégrer les lois de Bingham à SHALTOP. Les premiers résultats obtenus sont cohérents avec les comportements attendus, mais une analyse mathématique reste nécessaire pour préciser le cadre de validité théorique du modèle et le comparer à d’autres codes, comme VOLCFLOW ou R-AVAFLOW. Deux sites ont été choisis pour déterminer alors les limites opérationnelles des codes et leurs atouts par rapport à des outils plus empiriques tels que FLOW-R. Le premier, en Champagne, nous fournit une base de données d’une dizaine de mouvements sablo-argileux. Il permettra une approche statistique pour calibrer les paramètres et tester la reproductibilité des simulations. Le deuxième site est la rivière du Prêcheur, en Martinique, où de nombreux lahars sont intervenus depuis Janvier 2018.

Orateur: Marc Peruzzetto (IPGP / BRGM)

Transparents peruzzetto_topo_curvature.pdf

4 THE INCOMPRESSIBLE NAVIER-STOKES SYSTEM WITH FREE SURFACE AND VARIABLE DENSITY

We are interested in the numerical approximation of hydrostatic free surface flows with variable density. Such variable density flows occur when fresh water and sea water mix, in estuaries for instance; or when cold water mixes with warm water. We begin by writing the Navier-Stokes model with variable density, where the local density is a function of a tracer. A multilayer discretization of the system is performed, for which an energy balance is obtained. A kinetic interpretation of the multilayer system then allows to formulate a finite volume kinetic scheme. The numerical properties of the scheme are studied. 3D simulations are shown. One of our applications is the flow occurring when a tide lock between sea water and fresh water opens.

Orateur: Léa Boittin (Inria ; CEREMA ; Sorbonne Université, LJLL ; CNRS UMR 7598)

Transparents boittin_variabledensity.pdf

19:00 Dîner

mardi 19 juin

5 Fluides modèles versus fluides réels : de la difficulté à confronter expériences de laboratoire et modélisations pour les fluides complexes.

Orateur: Guillaume Chambon (IRSTEA)

Transparents Chambon.pdf

10:00 Pause café

Session 2: 3 exposés de 30 minutes

3 exposés de 30mn

6 Interaction vague-structure pour des modèles d'ondes longues en présence d'un objet en translation au fond

Nous présentons de nouveaux résultats concernant un problème d'interaction fluide-structure. Nous considérons le problème de Cauchy pour l'équation des vagues dans le cas où le domaine occupé par le fluide est à surface libre et avec un fond plat sur lequel un objet solide se translate horizontalement sous l'effet de la force de pression du fluide. Nous examinons deux systèmes asymptotiques décrivant le cas d’un fluide parfait incompressible en faible profondeur correspondant aux équations de Saint-Venant et de Boussinesq. Nous décrivons le système couplé dans ces deux régimes asymptotiques afin d'établir des résultats d'existence et d'unicité pour des données régulières (au sens de Sobolev). En particulier, un théorème d'existence en temps long est démontré, en étendant des anciens résultats. Afin de déterminer le mouvement du solide, une analyse précise des termes asymptotiquement singuliers induits par les forces de frottements est nécessaire. Ces travaux théoriques sont complémentés par une étude numérique approfondie. Les effets d'un solide capable de bouger au fond ont été mesurés par une suite de simulations basées sur un schéma de différences finies d'ordre élévé, adapté à ce problème couplé. Nous observons en particulier des transformations de vagues qualitativement différent ainsi que des effets d'amortissement dû au frottement.

Orateur: Krisztian Benyo (Université de Bordeaux)

Transparents Benyo_egrin_2018.pdf

7 Contrôle optimal sous contrainte d'un modèle hydrogéologique : un problème de pollution des eaux en sous-sol

Ce travail s'inscrit dans un contexte de contrôle de la pollution d'origine agricole des ressources en eau, en alliant modélisation économique et hydrogéologique. Pour cela, on considère un problème de contrôle optimal de contamination d'eau souterraine dans le cas d'un nécessaire compromis économique entre l'utilisation du polluant et les coûts de dépollution. Cet objectif économique est sous la contrainte d'un modèle hydrogéologique pour la propagation de la pollution dans l'aquifère. La modélisation du transport du polluant, dans un domaine 3D, revient à modéliser l'écoulement de fluides miscibles et incompressibles dans un milieu poreux. Ce modèle est constitué d'une équation aux dérivées partielles parabolique non linéaire (réaction-convection-dispersion) couplée par le tenseur de dispersion et le terme de convection à une équation elliptique. L'opérateur de dispersion dépend non linéairement de la vitesse du fluide qui est elle-même une inconnue du problème dépendant de la charge hydraulique. On choisira des conditions aux bords variées. Des résultats génériques sont donnés ([1]), notamment un résultat d'existence et de contrôlabilité. Puis un cas particulier est traité : nous prenons en compte la faible concentration du polluant dans le sous-sol et écrivons rigoureusement le modèle mis à l'échelle approprié et nous montrons l'existence et l'unicité de sa solution en utilisant des perturbations singulières et des outils d'analyse asymptotique ([2]). Quelques résultats numériques (2D en espace, issus d'une discrétisation par éléments finis mixtes) illustreront ces résultats analytiques. [1] E. Augeraud-Véron, C. Choquet, É. Comte. Optimal control for a Groundwater Pollution Ruled by a Convection-Diffusion-Reaction Problem, Journal of Optimization Theory and Applications, 173(3), 941-966, 2017. [2] E. Augeraud-Véron, C. Choquet, É. Comte. Existence, uniqueness and asymptotic analysis of optimal control problems for a groundwater pollution. "Accepté avec corrections mineures dans Control, Optimisation and Calculus of Variations.

Orateur: Éloïse COMTE (Laboratoire MIA, La Rochelle)

Transparents COMTE_Eloise.pdf

8 Floating structures in shallow water: local well-posedness in the axisymmetric case

The floating structure problem describes the interaction between surface water waves and a floating body, generally a boat or a wave energy converter. As shown by Lannes the equations for the fluid motion can be reduced to a set of two evolution equations on the surface elevation and the horizontal discharge. The presence of the object is accounted for by a constraint on the discharge under the object; the pressure exerted by the fluid on this object is then the Lagrange multiplier associated with this constraint. Our goal is to prove the well-posedness of this fluid-structure interaction problem in the shallow water approximation under the assumption that the flow is axisymmetric without swirl. We write the fluid equations as a quasilinear hyperbolic mixed initial boundary value problem and the solid equation as a second order ODE coupled to the fluid equations. Finally we prove the local in time well-posedness for this coupled problem, provided some compatibility conditions on the initial data are satisfied. References: [1] E. BOCCHI, Floating structures in shallow water: local well-posedness in the axisymmetric case, arXiv preprint (2018)

Orateur: Edoardo Bocchi (Institut de Mathématiques de Bordeaux)

Transparents bocchi-floatingstructure.pdf

12:00 Déjeuner

9 Des granulaires aux suspensions - prise en compte des interactions proches dans les simulations numériques

Orateur: Aline Lefebvre-Lepot (CNRS / CMAP-Ecole Polytechnique)

Transparents Lefebvre_EGRIN_180618-2-Suspensions.pdf

15:00 Pause café

Session 3: 3 exposés de 30 minutes

10 Un schéma numérique pour les écoulements viscoplastiques à densité variable.

Nous définissons et étudions un nouveau schéma numérique de semi-discrétisation en temps pour des écoulements incompressible visco-plastiques avec une rhéologie de Bingham et à densité variable. Dans un tel modèle, le tenseur des contraintes plastiques n'est pas différentiable dans les zones rigides. Nous proposerons une formulation sous forme de projection du tenseur des contraintes plastiques, que nous couplerons à une méthode de type pas fractionnaires initialement introduite pour les écoulements Newtoniens à densité variable. L'utilisation d'une vitesse à divergence nulle pour convecter la densité dans l'équation de conservation de la masse nous permet d'obtenir des bornes inférieures et supérieures positives sur la densité, qui seront essentielles pour l'analyse du schéma, dont la stabilité et la convergence seront présentées.

Orateur: Rénald Chalayer (Université Clermont Auvergne)

Transparents renald-egrain.pdf

11 An elasto-brittle model for sea-ice flow

This paper presents a first implementation of a new rheological model for sea ice on geophysical scales. The continuum model [1,2] is based on coupling between a progressive **damage** mechanism, with a Mohr-Coulomb **yield stress** damage criterion and a Maxwell **viscoelastic** constitutive equation. The model is tested on the basis of its capability to reproduce the complex mechanical and dynamical behavior of sea ice drifting through a narrow passage. Idealized as well as realistic simulations of the flow of ice through Nares Strait are presented. These demonstrate that the model reproduces the formation of stable ice bridges as well as the stoppage of the flow, a phenomenon occurring within numerous channels of the Arctic. In agreement with observations, the model captures the propagation of damage along narrow arch-like kinematic features, the discontinuities in the velocity field across these features dividing the ice cover into floes, the strong spatial localization of the thickest, ridged ice, the presence of landfast ice in bays and fjords and the opening of polynyas downstream of the strait. [1] V. Dansereau, J. Weiss, P. Saramito, P. Lattes and E. Coche. Ice bridges and ridges in the Maxwell-EB sea ice rheology. Cryosphere, 2017 [2] V. Dansereau, J. Weiss, P. Saramito and P. Lattes. A Maxwell-elasto-brittle rheology for sea ice modelling. Cryosphere, 2016.

Orateur: Pierre SARAMITO

Transparents saramito-banquise.pdf

12 Laminar shallow viscoplastic fluid flowing through an array of vertical obstacles

A new Bingham-Darcy shallow depth approximation flow model is proposed in this paper. This model is suitable for a shallow viscoplastic fluid flowing on a general topography and crossing an array of vertical obstacles. An analogous porous medium is first introduced to reduce the array of obstacles. The reduction model is based on a continuum model similar to the Brinkman equations, where the usual Darcy model is extended for viscoplastic Bingham fluids. A specific asymptotic analysis of this Bingham-Darcy porous medium for the case of shallow depth flows allows us to produce a new reduced model. The resulting solution is a highly nonlinear parabolic equation in terms of the flow height only, and is efficiently solved by a Newton method, without any regularization. However, our numerical predictions compares well, both qualitatively and quantitatively with both experimental measurements and full tridimensional simulations. Finally, a new experiment for a viscoplastic flow over an inclined plane through a network of obstacles is proposed and numerical simulations are provided for future comparison with experiments.

Orateur: Noé Bernabeu (LJK)

Transparents Bernabeu-lava.pdf

19:00 Dîner

mercredi 20 juin

13 Formulations augmentées en mécanique des fluides

Durant ce mini-cours, on montra l'importance d'augmenter certains systèmes d'EDPs en mécanique des fluides pour traiter certains problèmes théoriques et numériques: existence, stabilité, perturbations singulières seront par exemple au programme.

Orateur: Didier Bresch (LAMA, Université Savoie Mont Blanc)

Transparents Bresch_EGRIN.pdf

10:00 Pause café

14 Fluides modèles versus fluides réels : de la difficulté à confronter expériences de laboratoire et modélisations pour les fluides complexes.

Orateur: Guillaume Chambon (IRSTEA)

Transparents Chambon.pdf

12:00 Déjeuner

Session 4: 2 exposés de 30 minutes

2 exposés de 30mn

15 A double coordinate system for submarine avalanches modelling

The main goal of this work is to deal with the simulation of immersed granular avalanches. This kind of problems has been treated through averaged models following the pioneer work of Savage and Hutter [Acta Mech. 86, 1991], where a shallow water model is proposed to study dry aerial avalanches. This model has been successfully applied to simulate real and laboratory experiments. In [Bouchut, Fernández-Nieto, Mangeney, Lagrée. Acta Mech. 199, 2008], a Savage-Hutter type model has been proposed taking into account the curvature of a general bottom. Thus, the avalanche is described using local coordinates in terms of the bottom. In the case of submarine avalanches it is necessary to take into account the interstitial fluid (see [Iverson, Denlinger. J. Geophys. Re. 106, 2001]) but in this work we focus on the coordinate system in the derivation of the model. Thus, in the case of a submarine avalanche, we consider a water top layer and a submerged granular layer, that can be described using only one coordinate system (Cartesian or local coordinates). Nevertheless, this is not appropriate to correctly describe the behavior of both, water and granular layers. In this work we present the derivation of a new two-layer shallow model of Savage-Hutter type to study submarine avalanches. Our approach consider two different coordinate systems to deal with the modelling of both, the fluid and the granular layers over a fixed bottom. The fluid layer is described in Cartesian coordinates; based on previous works [Bouchut et al. 2008 and Fernández-Nieto, Vigneaux. Sema Semai Springer Series 3, 2014] and a change of variables from Cartesian to local coordinates is performed for the description of the granular layer. Coulomb friction law is imposed at the bottom and we also consider the friction between the fluid and the granular material. The latter is defined in such a way the obtained model accounts with a dissipative energy balance. Finally, we check the validity of the model with several numerical tests and, in particular, the results are compared to laboratory experiments.

Orateur: Gladys Narbona-Reina (Université de Séville)

Transparents narbona_egrin.pdf

16 Modélisation et simulation d'un écoulement pyroclastique par un écroulement de colonne granulaire fluidisée

Les écoulements pyroclastiques font partie des menaces volcaniques les plus dangereuses. Ce sont des avalanches à très haute température de cendres, de ponces, de fragments de roches et de gaz qui descendent à des vitesses de 100km/h ou plus, vers les parties basses du volcan. Les écoulements pyroclastique peuvent se propager à des distances de plus de 20km de leur point départ. Les raisons expliquant cette longue distance de propagation ne sont pas encore totalement connues et font l'objet plusieurs travaux de modélisation, de simulation et d'expérience dans des laboratoires. Oliver Roche dans [1] donne une perspective expérimentale basée sur un écroulement de colonne granulaire fluidisée, où il montre expérimentalement qu'en fluidisant une colonne granulaire, on introduit une pression dite interstitielle p_f qui fait flotter légèrement les grains et permet suite à un écroulement de la colonne, de les faire glisser à une distance d'environ deux fois plus importante que dans le cas non fluidisé. Nous proposons un modèle mathématique de fluide diphasique, basé sur les équations de Navier-Stokes incompressible qui permet de modéliser cette pression interstitielle et son effet dans l'écroulement d'une colonne granulaire. L'évolution de la pression interstitielle est modélisée par une équation de convection diffusion tandis que le déplacement des grains est modélisé par un modèle de rhéologie de type Drucker-Prager dont le seuil de plasticité dépend de la pression interstitielle p_f. Nous utilisons un schéma de volumes finis pour la discrétisation en espace et un schéma de bi-projection [2] pour la discrétisation en temps. Nous proposons aussi des cas tests numériques permettant de vérifier si le modèle proposé reproduit les caractéristiques observées expérimentalement. [1] Roche Olivier. Depositional processes and gas pore pressure in pyroclastic flows: an experimental perspective. Bulletin of Volcanology, 74:1807--1820, 2012. [2] Chupin, Laurent and Dubois, Thierry. A bi-projection method for Bingham type flows. Computers & Mathematics with Applications, 72:1263--1286, 2016.

Orateur: Charlie Douanla Lontsi

Transparents granular_flow_charlie_talk.pdf

19:30 Apéritif

20:00 Dîner

jeudi 21 juin

17 Formulations augmentées en mécanique des fluides

Durant ce mini-cours, on montra l'importance d'augmenter certains systèmes d'EDPs en mécanique des fluides pour traiter certains problèmes théoriques et numériques: existence, stabilité, perturbations singulières seront par exemple au programme.

Orateur: Didier Bresch (LAMA, Université Savoie Mont Blanc)

Transparents Bresch_EGRIN.pdf

10:00 Pause café

Session 5: 3 exposés de 30 minutes

3 exposés de 30mn

18 Maxwell rencontre Saint-Venant à propos de fluides viscoélastiques

La modélisation des écoulements fluides non-Newtoniens reste un sujet de recherche actif depuis les travaux pionniers de Maxwell en viscoélasticité. Dans l'exposé, on discutera de modèles récents, dans le cadre des écoulements hydrostatiques à surface libre introduit historiquement par Saint-Venant. Puis on compare numériquement deux modèles qui diffèrent uniquement dans l'équation d'évolution du tenseur des efforts (par des termes de la dérivée d'un tenseur utilisant le gradient des vitesses). Ce sont deux systèmes hyperboliques non linéaires qu'on simule avec des approximations volumes finis grâce à une nouvelle méthode de relaxation. Un solveur de Riemann entropique, de type Suliciu, a été construit dans ce but.

Orateur: Sébastien Boyaval (Ecole des Ponts ParisTech, Laboratoire d'hydraulique Saint-Venant)

Transparents boyaval_viscoelastic.pdf

19 A tensorial model for suspensions of non-colloidal rigid particles

La modélisation mathématique des suspensions de particules solides présente de nombreuses applications, notamment la prévention des risques naturels, causés par des coulées de débris et ou des laves torrentielles par exemple. Certains modèles quasi-newtoniens ont donné de bons résultats en cisaillement simple et en régime stationnaire mais, la microstructure n'est modélisée que par une variable scalaire, la fraction volumique. Afin de modéliser des effets transitoires et de considérer des géométries plus complexes, nous proposons un modèle couplant les équations de Navier-Stokes incompressibles avec un tenseur de structure vérifiant une équation aux dérivées partielles hyperbolique non-linéaire. Ainsi, l'anisotropie de la microstructure sous cisaillement est modélisée. La viscosité apparente $\eta_{app}$ est tracée de la déformation $\gamma$ lors d'une inversion de cisaillement présente un comportement non trivial prédit correctement par le modèle. Celui-ci est aussi en mesure de donner des prédictions sur la fonction de distribution de paire en régime stationnaire. La probabilité $g(\theta)$ pour une particule d'avoir une particule voisine dans la direction $\theta\in [0,2\pi]$ n'est pas uniforme pour une suspension en cisaillement. L'angle de déplétion correspondant au minimum est bien retrouvé, plus généralement, l'allure des observations est correctement prédite par le modèle. Le modèle est étendu afin de prédire des contraintes normales réalistes. Celles-ci sont calculées du fait de la présence d'une dérivée objective de type Gordon-Schowalter dans l'équation d'évolution du tenseur de structure au lieu d'être postulées comme dans les modèles quasi-newtoniens troisième figure présente la comparaison entre nos prédictions et des résultats expérimentaux pour la seconde différences des contraintes normales en régime stationnaire est quantitative. En conclusion, nous proposons un modèle continu pour les suspensions permettant des prédictions quantitatives aux échelles macroscopiques et microscopiques. Le bon comportement des différences de contrainte normale prédites ouvre la voie à des simulations en géométries complexes.

Orateur: Olivier Ozenda (LJK)

Transparents ozenda-slides-egrin-2018.pdf

12:00 Déjeuner

Transfert: Retour à Clermont-Ferrand