7ième école EGRIN
Septième école EGRIN
VVF Le Grand Lioran, 24-27 juin 2019
De nos jours, la prévention de catastrophes naturelles, la gestion des ressources d'eau ou encore l'impact des écoulements sur les sols et structures sont des questions d'importance socio-économique majeure. Le développement de modèles et d'outils de simulation numérique fiables et performants est essentiel à la compréhension des ces questions. Le GdR interdisciplinaire EGRIN a pour objectif de rassembler des chercheurs autour de ces thématiques pour échanger sur les avancées récentes, déterminer les verrous scientifiques existants et renforcer les collaborations.
Les exposés commenceront le lundi 24 juin en début d'après-midi et se termineront le jeudi 27 juin à midi.
Trois mini-cours sont prévus :
|
Cours I - Claire Chainais-Hillairet (Laboratoire Paul Painlevé, Lille) Schémas volumes finis pour des problèmes dissipatifs : étude du comportement en temps long. |
|
Dans ce cours, je m’intéresserai au comportement en temps long de quelques modèles présentant une structure dissipative. L’objectif est de bien comprendre cette structure des modèles continus pour obtenir ensuite des résultats similaires pour des schémas numériques de type volumes finis. |
|
Cours II - Franck Radjai (Laboratoire de Mécanique et Génie Civil, Montpellier) Modélisation et rhéologie des milieux granulaires. |
|
Dans ce cours, je propose une introduction aux concepts et modèles de base développés en physique et mécanique des milieux granulaires pendant les trente dernières années. Après une introduction à quelques notions de base, nous allons considérer les états d’équilibre statique d’un assemblage de grains et les variables de texture granulaire. Ensuite, nous étudierons la rhéologie quasi-statique et la théorie des états critiques comme le cadre général de la formulation des lois de comportement pour les milieux granulaires. Les modèles récents des écoulements inertiels seront présentés brièvement et étendus aux suspensions denses. On s’intéressera également aux modèles micromécaniques, aux milieux cohésifs et à l’influence des propriétés des particules (distributions des tailles, formes) sur le comportement à partir des résultats récents. La dernière partie du cours portera sur les méthodes de simulation de la dynamique des grains (dynamique moléculaire et dynamique des contacts). |
|
Cours III - Charlotte Perrin (Institut de Mathématiques de Marseille) Phénomènes de congestion dans les fluides. |
|
Le but de ce mini-cours est de donner quelques éléments d'analyse mathématique pour l'étude d'équations fluides sous une contrainte de densité maximale. Ce type de systèmes apparaît naturellement pour la prise en compte de phénomènes de saturation (ou congestion) dans les mélanges biphasiques tels que les suspensions granulaires, ou pour la dynamique d'écoulements partiellement en surface libre (écoulements en conduite fermée, structures flottantes, etc.). Sur le plan mathématique on s'intéressera à l'existence de solutions aux modèles proposés, la justification de limites singulières et à la discrétisation des équations. |
Progamme prévisionnel :
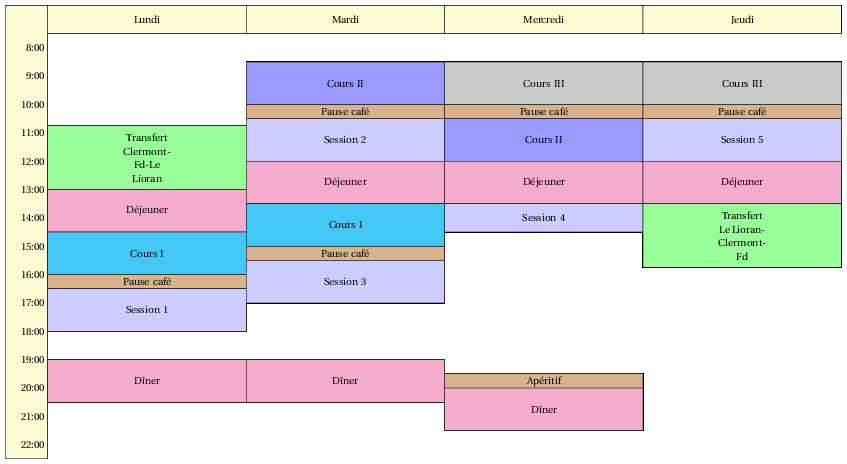
Organisation : L. Chupin, T. Dubois, C. Lucas, M.F. Grespier
Partenaires :





