Long time behaviour of quantum and classical systems
IRMAR
The goal of the meeting is to bring together people working on the three areas:
* many-body (linear) scattering (quantum and classical)
* non-linear quantum scattering
* non-linear classical scattering
and share techniques/ideas between communities. In particular, there will be three mini-courses given by Christian Gérard, Nicola Visciglia, and Daniel Han Kwan.
Organisation: Julien Sabin
Gestion des participants et des repas: Florian Rogowski et Aude Guiny
Supports financiers: ANR via la CPJ de Julien Sabin, Université de Rennes, IRMAR
Coming to IRMAR:
The math department (IRMAR) is situated on the Beaulieu campus of the Université de Rennes. You can reach it by bus, there are two possible bus stops near the department:
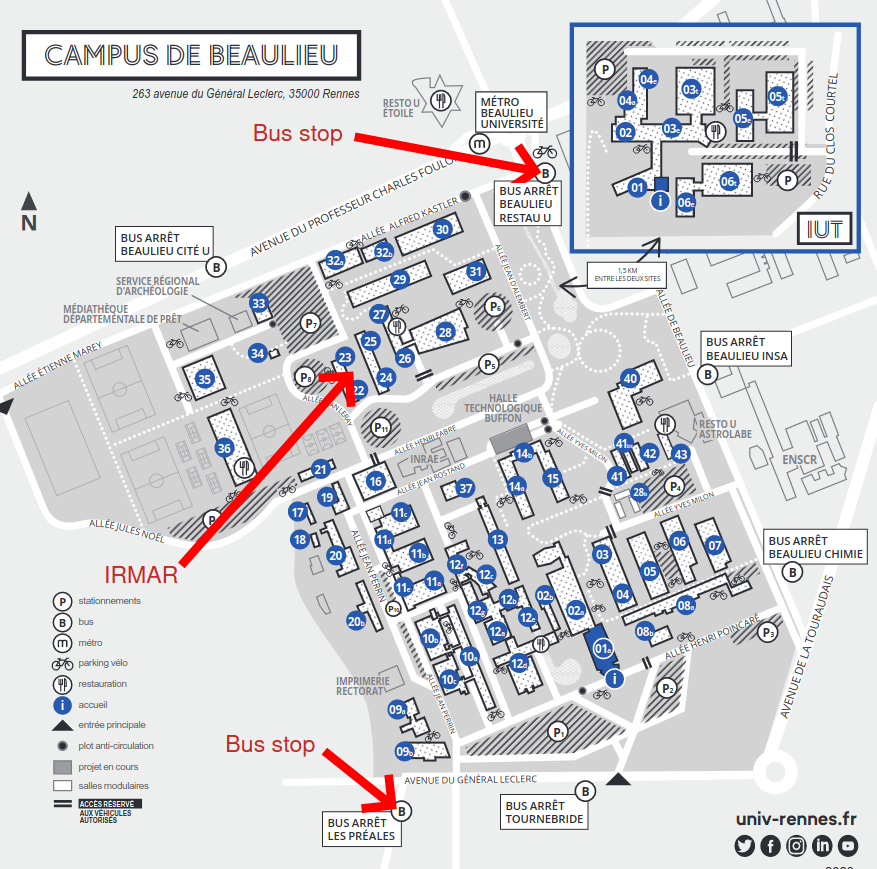
You can take either the bus C4 (direction Rennes/ZA Saint Sulpice) and stop at "Les préales" or "Beaulieu Université), or the bus C6 (direction Cesson-Sévigné) and stop at "Les préales". All the informations on public transportation in Rennes may be found here: https://www.star.fr/
For those staying at "Cité Internationale Paul Ricoeur", the closest bus stop is "Musée Beaux Arts".
All talks will be held at the ground floor of the IRMAR building, next to the coffee room. To enter the building, a badge a needed but since there are many people coming and going from the building all the time, you will be able to enter after waiting a bit.
