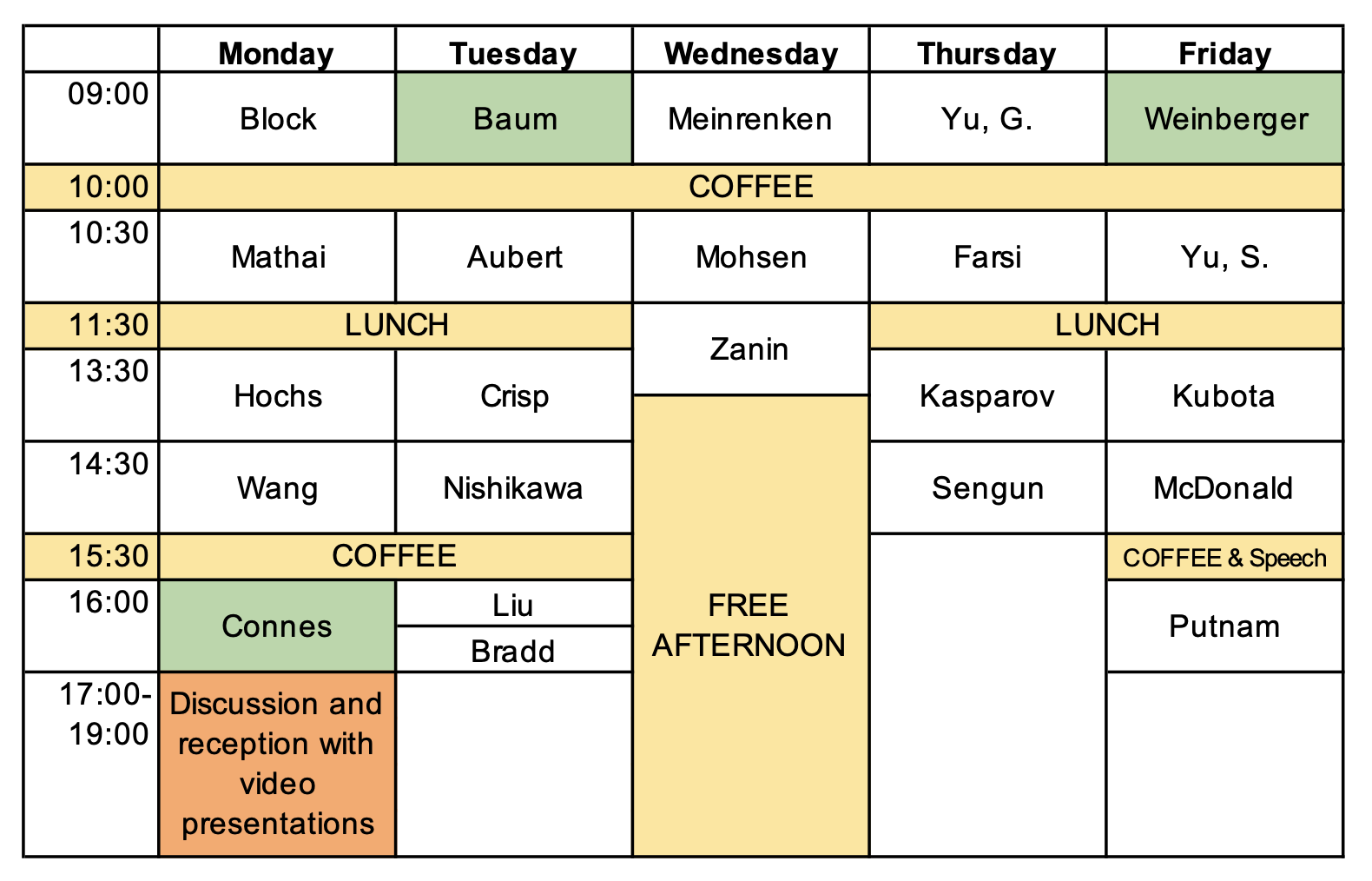
Titles & Abstracts
Anne-Marie Aubert (Sorbonne Université)
Title: Application of extended quotients to the Langlands program.
Abstract: We will first introduce the notion of extended quotient, which originates in noncommutative geometry. Next, we will explain how it naturally occurs in both the representation theory of p-adic reductive groups and the study of enhanced versions of local Langlands parameters. Finally, we will show how to interpret the local Langlands correspondence into a correspondence between extended quotients.
Paul Baum (Penn State University)
Title: To be confirmed.
Jonathan Block (University of Pennsylvania)
Title: From Index theory to representation theory.
Abstract: The Baum-Connes Conjecture is fundamental tool in the C*-algebraic approach to index theory. We describe a program that exports ideas and tools from Baum-Connes and index theory and applies them to various geometries.
Jacob Bradd (Penn State University)
Title: On the Casselman Schwartz algebra and the reduced group C^*-algebra of a real reductive group
Abstract: The Casselman Schwartz algebra S(G) of a real reductive group is a Fréchet algebra of smooth, very rapidly decreasing functions on G. It is not holomorphically closed in the reduced C*-algebra C*rG. In fact, S(G) is similar in many ways to the space of smooth compactly supported functions while C*rG is similar in many ways to L2(G). Despite the difference, we prove that these two algebras are assembled from similar component parts in similar ways, and have isomorphic K-theory. This uses both a strong understanding of the algebraic structure of S(G) (from Delorme's Paley-Weiner theorem), and the Oka principle, coming from the theory of several complex variables. Our results also give a new proof of the Connes-Kasparov isomorphism.
Alain Connes (Collège de France, IHES)
Title: From the metaphysics of F1 to representation theory via NCG
Abstract: I will speak about my joint work with C. Consani and H. Moscovici.
Tyrone Crisp (University of Maine)
Title: Towards a Mackey formula for families of principal series representations
Abstract: Mackey's classical intertwining-number formula, which computes the dimensions of spaces of intertwining operators between representations of a finite group G induced from a subgroup P, can be stated succinctly and conceptually as a decomposition of the group algebra CG as a CP-bimodule; the intertwining numbers between individual representations can then be obtained by taking tensor products with this bimodule. For tempered unitary representations of real reductive groups we know - thanks to work of Bruhat, Knapp-Stein, and many others - a great deal about intertwining operators between individual induced representations. In this talk I will describe a program, stemming from joint work with Pierre Clare and Nigel Higson, whose goal is to understand these intertwining operators "globally", for families of induced representations, by analysing certain bimodules over group C*-algebras.
Carla Farsi (University of Colorado Boulder)
Title: Bridge Builders, Noncommutative Metric Geometry and Inductive Limits.
Abstract: I will present some inductive limit constructions as associated to limits of metric spectral triples converging for the spectral propinquity of Latrémolière. Examples include noncommutative solenoids and Bunce-Deddens algebras.
We also discuss covariant constructions especially as associated to isometry groups of metric spectral triples.
Peter Hochs (Radboud University, Nijmegen)
Title: Equivariant analytic torsion and an equivariant Ruelle dynamical zeta function
Abstract: Analytic torsion was introduced by Ray and Singer as a way to realise Reidemeister-Franz torsion analytically. (The equality was independently proved by Cheeger and Müller.) The Ruelle dynamical zeta function is a topological way to count closed curves of flows on compact manifolds. The Fried conjecture states that, for a suitable class of flows, the Ruelle dynamical zeta function has a well-defined value at zero, and that the absolute value of this value equals analytic torsion. With Hemanth Saratchandran, we define equivariant versions of analytic torsion and of the Ruelle dynamical zeta function, for proper actions by locally compact groups, with compact quotients. These have some natural fundamental properties, generalising properties of their non-equivariant counterparts. The resulting equivariant version of Fried’s conjecture does not hold in general, but it does hold in some classes of examples. This motivates the search for general conditions under which the equivariant Fried conjecture is true.
Gennadi Kasparov (Vanderbilt University)
Title: Index theorem for orbitally elliptic operators
Abstract: For a proper action of a Lie group on a manifold, I will explain how to define the index of an orbital elliptic operator as an element of K-theory of the appropriate crossed product C*-algebra. The orbital index theorem is similar to the index theorem for usual elliptic operators but involves the orbital Dirac operator instead of the Dolbeault element.
Yosuke Kubota (Kyoto University)
Title: Lifting finite propagation operators and positive scalar curvature
Abstract: There are several known obstructions for closed spin manifolds to admit PSC metric, which are not the Rosenberg index itself but are derived from a Dirac operator. Such obstructions are often considered to be dominated by the Rosenberg index (Schick's meta-conjecture). In this talk, I explain that two of such obstructions, Hanke-Pape-Schick's codimension 2 submanifold index and Zeidler's KO-bandwidth, are dominated by the Rosenberg index as expected. The proof is given by the technique of lifting a finite propagation operator on a kind of non-compact manifold onto its covering space.
Shiqi Liu (Penn State University)
Title: "Ellipticity" of the hypoelliptic Laplacian
Abstract: Invented by Jean-Michel Bismut, the hypoelliptic Laplacian is a new type of ``index theory”. It provides a remarkable trace formula, and further reveals completely new insights in geometry and representation theory. However, the main difficulty of this subject lies in analysis. Especially, the hypoellipticity of the operator makes the analysis challenging. Recently, with techniques from noncommutative geometry, we show the hypoelliptic Laplacian is actually elliptic under a new calculus. This will significantly reduce the complexity of analysis as well as bring new understanding of algebraic structure of the hypoelliptic Laplacian.
In this talk, I will illustrate our innovation by discussing the circle case, and briefly explain how to reduce compact Lie group case to the circle case.
This is a joint work with N. Higson, E. MacDonald, F. Sukochev, and D. Zanin.
Edward McDonald (Penn State University)
Title: Introduction to the hypoelliptic Laplacian on a compact group
Abstract: For the past decade or more, J. M. Bismut has been working on the theory and applications of a one-parameter deformation of the Laplace operator which he calls the Hypoelliptic Laplacian. I will discuss the most accessible case of Bismut's theory, the hypoelliptic Laplacian on a compact group, and how his deformation techniques can be used to prove Frenkel's formula for the heat kernel. This talk is based on an ongoing project with N. Higson, S. Liu, F. Sukochev and D. Zanin.
Eckhard Meinrenken (University of Toronto)
Title: On the integration of transitive Lie algebroids
Abstract: Lie algebroids are the infinitesimal counterparts to Lie groupoids. On the other hand, not every Lie algebroid comes from a Lie groupoid. Following partial results by many authors, the precise obstructions to the integrability problem were obtained by Crainic-Fernandes in their 2003 Annals paper. In this talk, I will explain how to understand these obstructions in the special case of transitive Lie algebroids.
Omar Mohsen (Université d’Orsay)
Title: A C*-algebra proof of a theorem by Helffer and Nourrigat
Abstract: In 1979, Helffer and Nourrigat proved the Rockland conjecture which gives an equivalence between hypoellipticity of homogeneous differential operators and injectivity of the differential operators under unitary representations. Their proof relies on a very detailed and fine analysis of irreducible unitary representations of nilpotent Lie groups using the orbit method. I will present a proof which is based on C*algebras arguments and (almost completely) avoids using Kirillov's orbit method.
Shintaro Nishikawa (Universität Münster)
Title: BC for CAT(0)-Cubical Groups, Overview and Localization Approach
Abstract: I will provide an overview of a recently obtained new proof of the Baum—Connes conjecture with coefficients (BCC) for groups that act properly on a finite-dimensional CAT(0)-cube complex. This is a joint work with Brodzki, Guentner, and Higson. While the Higson-Kasparov theorem (2001) already covers the BCC for such groups as a special case, our new approach offers fresh insights and an entertaining perspective on understanding the traditional proof scheme of the BCC.
Ian Putnam (University of Victoria)
Title: Dynamics of translation surfaces and C*-algebras
Abstract: The study of translation surfaces is a very active area of dynamics. The objects of interest are 1-dimensional foliations of surfaces. I will give a brief (and imprecise) introduction to the subject. Recently, Kathryn Lindsey and Rodrigo Trevino gave a construction of translation surfaces from bi-infinite Bratteli diagrams. They also showed how this construction can produce surfaces of infinite genus displaying dynamics which does not appear in the finite genus case. I will discuss precise ways in which these foliations and their C*-algebras are related to the AF-algebras associated with the Bratteli diagrams. The emphasis of the talk will be on ways that operator algebras can enlighten the study of translation surfaces and, conversely, how important ideas from translation surfaces can be used in operator algebras. This is joint work with Rodrigo Trevino.
Haluk Sengun (University of Sheffield)
Title: Local theta correspondence via C*-algebras of groups
Abstract: Theta correspondence is a major theme in the theory of automorphic forms and in representation theory. The local version of the correspondence sets up a bijection between certain subsets of admissible duals of suitable pairs of reductive groups. There are two special cases in which the correspondence is known to enjoy extra features, the ‘equal rank’ case where temperedness is preserved and the ‘stable range’ case where unitarity is preserved.
In joint work with Bram Mesland (Leiden), we show that in these special cases, the local theta correspondence is actually given by a Morita equivalence of certain C*-algebras. There are interesting applications and some global questions that follow this result. Time permitting, I will discuss some of these.
Mathai Varghese (University of Adelaide)
Title: Index theory for small bundle gerbes
Abstract: Small bundle gerbes are essentially finite dimensional. We give explicit construction of such gerbes, which are generalizations of decomposable bundle gerbes studied in earlier work with I. M. Singer. We prove an Atiyah-Singer type theorem in this context, and give applications of our theorem. This is joint work with Richard B. Melrose.
Hang Wang (East China Normal University)
Title: Representation of connected Lie groups and covering groups
Abstract: Functoriality is a crucial philosophy in the study of relations between irreducible representations of different Lie groups or algebraic groups. In this talk, we compare irreducible unitary representations of two connected Lie groups where one is a cover of the other, in the context of operator algebras and K-theory. This is joint work with Kuok Fai Chao.
Shmuel Weinberger (University of Chicago)
Title: Bounded geometry and low dimensional homotopy complex projective spaces.
Abstract: We will study manifolds homotopy equivalent to CP^3 and CP^4 and use our analysis to give bounded geometry triangulations of S^7 that only bound bounded geometry triangulated balls that have a quadratic number of simplices. This implies that the isomorphism between surgery theory and the fiber of the assembly map is (in the smooth setting) "quantitatively nonlinear".
Guoliang Yu (Texas A&M University)
Title: An index theorem for manifolds with polyhedral boundary and scalar curvature rigidity
Abstract: I will explain how to apply an index theorem for Dirac operators on manifolds with polyhedral boundary to solve Gromov's dihedral extremality conjecture on scalar curvature for polyhedra. This is joint work with Jinmin Wang and Zhizhang Xie.
I would like to take this special opportunity to acknowledge Nigel's great influence and inspiration on my mathematical career over the span of the last 30 years.
Shilin Yu (Xiamen University)
Title: Deformations of representations
Abstract: I will explain how to extend the philosophy of the Mackey analogy, due to Mackey, Higson and Afgoustidis, to the case of non-tempered representations of reductive Lie groups. The observation is that the celebrated coadjoint orbit method, proposed by Kirillov and Kostant, are very similar to the Mackey analogy in nature, when both are viewed as statements about deformations of representations. This gives a new approach to Vogan's conjecture about quantizations of nilpotent orbits.
The talk is based on joint work with Conan Leung and ongoing project with Ivan Losev.
Dmitriy Zanin (University of New South Wales)
Title: Principal symbol mapping on contact manifolds: the C*-algebraic approach
Abstract: The principal symbol of a (pseudo-differential) operator is, typically, not defined but postulated and this does not look nice for an operator theorist. In the setting of Heisenberg groups, the co-domain of the principal symbol is usually an algebra of functions equipped with an ad hoc product.
The C*-algebraic approach defines a principal symbol mapping as a (surjective) *-homomorphism of C*-algebras. In the case of a Heisenberg group , the co-domain of the principal symbol mapping is a very natural algebra of operators.
It appears that the principal symbol mapping behaves equivariantly under Heisenberg diffeomorphisms. This allows to extend the notion of the principal symbol mapping to contact manifolds (by the patching process).
A very general version of Connes’ trace formula (for sub-Riemannian manifolds) is proved. In particular, spectrally correct sub-Riemannian volume is explicitly written.
