Journées Statistiques du Sud 2024

Programme scientifique

Le but de ces journées est de donner une vue d'ensemble des développements scientifiques récents en statistique et de promouvoir les échanges entre étudiants diplômés, chercheurs confirmés.

Programme de la conférence et recueil des résumés :
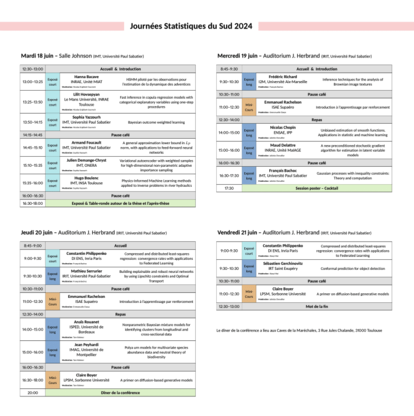
  ➤ Journées Statistiques du Sud 2024

Mini-cours

2 x 1h30

Claire Boyer - LPSM, Sorbonne Université - Jeudi 20/06 à 16h30 et Vendredi 21/06 à 11h
A primer on diffusion-based generative models

Emmanuel Rachelson - ISAE Supaéro - Mercredi 19/06 à 11h et Jeudi 20/06 à 11h
Introduction à l'apprentissage par renforcement

Exposés longs

45 min + 15 min questions

François Bachoc - ENSAE, Institut Polytechnique de Paris - Mercredi 19/06 à 16h30
Unbiased estimation of smooth functions, Applications in statistic and machine learning

Given a smooth function f, we develop a general approach to turn Monte Carlo samples with expectation m into an unbiased estimate of f(m). Specifically, we develop estimators that are based on randomly truncating the Taylor series expansion of f and estimating the coefficients of the truncated series. We derive their properties and propose a strategy to set their tuning parameters -- which depend on m -- automatically, with a view to make the whole approach simple to use. We develop our methods for the specific functions f(x)=log(x) and f(x)=1/x, as they arise in several statistical applications such as maximum likelihood estimation of latent variable models and Bayesian inference for un-normalised models. Detailed numerical studies are performed for a range of applications to determine how competitive and reliable the proposed approach is.

Nicolas Chopin - ENSAE, Institut Polytechnique de Paris - Mercredi 19/06 à 14h
Unbiased estimation of smooth functions, Applications in statistic and machine learning

Given a smooth function f, we develop a general approach to turn Monte Carlo samples with expectation m into an unbiased estimate of f(m). Specifically, we develop estimators that are based on randomly truncating the Taylor series expansion of f and estimating the coefficients of the truncated series. We derive their properties and propose a strategy to set their tuning parameters -- which depend on m -- automatically, with a view to make the whole approach simple to use. We develop our methods for the specific functions f(x)=log(x) and f(x)=1/x, as they arise in several statistical applications such as maximum likelihood estimation of latent variable models and Bayesian inference for un-normalised models. Detailed numerical studies are performed for a range of applications to determine how competitive and reliable the proposed approach is.

Maud Delattre - INRAE, Unité MaIAGE - Mercredi 19/06 à 15h
A new preconditioned stochastic gradient algorithm for estimation in latent variable models.

Latent variable models are powerful tools for modeling complex phenomena involving in particular partially observed data, unobserved variables or underlying complex unknown structures. Inference is often difficult due to the latent structure of the model. To deal with parameter estimation in the presence of latent variables, well-known efficient methods exist, such as gradient-based and EM-type algorithms, but with practical and theoretical limitations. We propose as an alternative for parameter estimation an efficient preconditioned stochastic gradient algorithm. Our method includes a preconditioning step based on a positive definite Fisher information matrix estimate. We prove convergence results for the proposed algorithm under mild assumptions for very general latent variables models. We illustrate through relevant simulations the performance of the proposed methodology in a nonlinear mixed effects model and in a stochastic block model.

Sébastien Gerchinovitz - IRT Saint Exupéry - Vendredi 21/06 à 9h30
Conformal prediction for object detection

We address the problem of constructing reliable uncertainty estimates for object detection. We build upon classical tools from Conformal Prediction, which offer (marginal) risk guarantees when the predictive uncertainty can be reduced to a one-dimensional parameter. In this talk, we will first recall standard algorithms and theoretical guarantees in conformal prediction and beyond. We will then address the problem of tuning a two-dimensional uncertainty parameter, and will illustrate our method on an objection detection task. This is a joint work with Léo Andéol, Luca Mossina, and Adrien Mazoyer.

Jean Peyhardi - IMAG, Université de Montpellier - Jeudi 20/06 à 15h
Polya urn models for multivariate species abundance data: Properties and application

This talk focuses on models for multivariate count data, with emphasis on species abundance data. Two approches emerge in this framework: the Poisson log-normal (PLN) and the Tree Dirichlet multinomial (TDM) models. The first uses a latent gaussian vector to model dependencies between species whereas the second models dependencies directly on observed abundances. The TDM model makes the assumption that the total abundance is fixed, and is then often used for microbiome datasets since the sequencing depth (in RNA seq) varies from one observation to another, leading to a total abundance that is not really interpretable. We propose to generalize TDM models in two ways: by relaxing the fixed total abundance assumption and by using Polya distribution instead of Dirichlet multinomial. This family of models corresponds to Polya urn models with a random number of draws and will be named Polya splitting distributions. In a first part I will present the probabilistic properties of such models, with focus on marginals and probabilistic graphical model. Then it will be shown that these models emerge as stationary distributions of multivariate birth death process under simple parametric assumption on birth-detah rates. These assumptions are related to the neutral theory of biodiversity that assumes no biological interaction between species. Finally the statistical aspects of Polya splitting models will be presented: the regression framework, the inference, the consideration of a partition tree structure and two applications on real data.

Anaïs Rouanet - ISPED, Université de Bordeaux - Jeudi 20/06 à 14h
Nonparametric Bayesian mixture models for identifying clusters from longitudinal and cross-sectional data

The identification of sets of co-regulated genes that share a common function is a key question of modern genomics. Bayesian profile regression is a semi-supervised mixture modelling approach that makes use of a response to guide inference toward relevant clusterings. Previous applications of profile regression have considered univariate continuous, categorical, and count outcomes. In this work, we extend Bayesian profile regression to cases where the outcome is longitudinal (or multivariate continuous), using multivariate normal and Gaussian process regression response models. The model is applied on budding-yeast data to identify groups of genes co-regulated during the Saccharomyces cerevisiae cell cycle. We identify four distinct groups of genes associated with specific patterns of gene expression trajectories, along with the bound transcriptional factors, likely involved in their co-regulation process.

Frédéric Richard - I2M, Université Aix-Marseille - Mercredi 19/06 à 9h30
Inference techniques for the analysis of Brownian image textures

In this talk, I will present some techniques for estimating the functional parameters of anisotropic fractional Brownian fields, and their application to the analysis of image textures. I will focus on a first approach based on the resolution of inverse problems which leads to a complete estimation of parameters. The formulation of these inverse problems comes from the fitting of the empirical semi-variogram of an image to the semi-variogram of a turning band field that approximates the anisotropic fractional Brownian field. It takes the form of a separable non-linear least square criterion which can be solved by a variable projection method, and extended to take into account additional penalties. Besides, I will also describe an alternate approach which uses neural networks to obtain accurate estimation of field features such as the field degree of regularity.

Mathieu Serrurier - IRIT, Université Paul-Sabatier - Jeudi 20/06 à 9h30
Building explainable and robust neural networks by using Lipschitz constraints and Optimal Transport

The lack of robustness and explainability in neural networks is directly linked to the arbitrarily high Lipschitz constant of deep models. Although constraining the Lipschitz constant has been shown to improve these properties, it can make it challenging to learn with classical loss functions. In this presentation, we explain how to control this constant, and demonstrate that training such networks requires defining specific loss functions and optimization processes. To this end, we propose a loss function based on optimal transport that not only certifies robustness but also converts adversarial examples into provable counterfactual examples.

Exposés courts

20 min + 10 min questions

Marie Chion - MRC Biostatistics Unit, University of Cambridge - Vendredi 21/06 à 9h
A Bayesian Framework for Multivariate Differential Analysis accounting for Missing Data

Current statistical methods in differential proteomics analysis generally leave aside several challenges, such as missing values, correlations between peptide intensities and uncertainty quantification. Moreover, they provide point estimates, such as the mean intensity for a given peptide or protein in a given condition. The decision of whether an analyte should be considered as differential is then based on comparing the p-value to a significance threshold, usually 5%. In the state-of-the-art limma approach, a hierarchical model is used to deduce the posterior distribution of the variance estimator for each analyte. The expectation of this distribution is then used as a moderated estimation of variance and is injected directly into the expression of the t-statistic. However, instead of merely relying on the moderated estimates, we could provide more powerful and intuitive results by leveraging a fully Bayesian approach and hence allow the quantification of uncertainty.
This talk introduces this idea by taking advantage of standard results from Bayesian inference with conjugate priors in hierarchical models to derive a methodology tailored to handle multiple imputation contexts. Furthermore, we aim to tackle a more general problem of multivariate differential analysis, to account for possible inter-peptide correlations. By defining a hierarchical model with prior distributions on both mean and variance parameters, we achieve a global quantification of uncertainty for differential analysis. The inference is thus performed by computing the posterior distribution for the difference in mean peptide intensities between two experimental conditions. In contrast to more flexible models that can be achieved with hierarchical structures, our choice of conjugate priors maintains analytical expressions for direct sampling from posterior distributions without requiring expensive MCMC methods.

Constantin Philippenko - DI ENS, Inria Paris - Jeudi 20/06 à 9h
Compressed and distributed least-squares regression: convergence rates with applications to Federated Learning

We investigate the impact of compression on stochastic gradient algorithms for machine learning, a technique widely used in distributed and federated learning.
We underline differences in terms of convergence rates between several unbiased compression operators, that all satisfy the same condition on their variance, thus going beyond the classical worst-case analysis. To do so, we focus on the case of least-squares regression (LSR) and analyze a general stochastic approximation algorithm for minimizing quadratic functions relying on a random field. More particularly, we highlight the impact on the convergence of the covariance of the additive noise induced by the algorithm. We consider weak assumptions on the random field, tailored to the analysis (specifically, expected Hölder regularity), and on the noise covariance, enabling the analysis of various randomizing mechanisms, including compression. We then extend our results to the case of federated learning.

Session poster

Victoria Bruning, Tom Rohmer. [Plus de details]
Copula Integration for Genetic Selection Parameter Estimation in Bivariate Linear Mixed Models

El Mehdi Achour, Armand Foucault, Sébastien Gerchinovitz, François Malgouyres. [Plus de details]
A general approximation lower bound in Lp norm, with applications to feed-forward neural networks

Jean Baccou, Francçois Bachoc, Florian Gossard. [Plus de details]
Statistiques et machine learning pour la prédiction de sorties complexes avec application à la sûreté nucléaire.

David Heredia, Aldéric Joulin, Olivier Roustant. [Plus de details]
Global sensitivity analysis with weighted Poincaré inequalities

Sophia Yazzourh. [Plus de details]
Integration of medical knowledge into reinforcement learning for dynamic treatment regimes

Nicolas Enjalbert Courrech. [Plus de details]
IIDEA : Interactive Inference for Differential Expression Analyses

Pré-journée pour les étudiant.es

20 min + 5 min questions

Hanna Bacave - INRAE, Unité MIAT - Mardi 18/06 à 13h
HSMM piloté par les observations pour l'estimation de la dynamique des adventices

Les adventices sont des plantes qui poussent spontanément dans les parcelles agricoles et qui entrent en compétition avec les cultures. Leur dynamique repose sur la colonisation et la dormance. La banque de graines n'étant jamais observée de manière naturelle, une modélisation de cette dynamique a été proposée dans le cadre des Hidden Markov Models (HMM). Ce modèle, appelé Observation Driven-HMM (OD-HMM) étend les HMM au cas où les probabilités de transition dépendent de l'observation courante pour tenir compte des nouvelles graines produites qui entrent dans la banque de graines. Cependant, pour plus de réalisme sur la distribution de la survie de la banque de graines, le cadre naturel serait celui des Hidden Semi-Markov Models (HSMM). Néanmoins la notion de durée de séjour dans l'état caché n'est plus adaptée dès lors que l'observation influence la chaîne cachée à chaque instant. En nous appuyant sur les deux cadres OD-HMM et HSMM, nous proposons un nouveau modèle général : l'OD-HSMM, permettant à la fois de tenir compte d'une influence des données sur la chaîne cachée et de s'affranchir de la loi du temps de séjour géométrique. Nous en présentons une version paramétrique à partir des paramètres clés de la dynamique d'une espèce adventice et nous discutons différentes approches pour leur estimation.

Hugo Boulenc - IMT, INSA Toulouse - Mardi 18/06 à 15h35
Physics-Informed Machine Learning methods applied to inverse problems in river hydraulics

Faced with the socio-economic challenges of flood forecasting, in a context of climate change, multi-scale modeling approaches that take advantage of the maximum amount of information available are needed to enable accurate and rapid flood forecasts.
In this context, the objective of this work is to develop a Physics-Informed Machine Learning method to efficiently perform flood models calibration, which is crucial to ensure accurate forecasts. More precisely, an approach aiming at inferring a spatially-distributed friction coefficient (Manning-Strickler coefficient) from data with a Physics-Informed Neural Network is proposed. The method consists in considering for the loss function a physical model term corresponding to the 2D Shallow-Water Equations residual and a data discrepancy term. Data are generated with the reference software DassFlow1 and refer to observations of the free surface height and mass flow rate at various locations and times in the computational domain. The PINN parameters and the spatially-distributed friction parameter are then optimized so that the weighted sum of the physical residual term and the data discrepancy term are minimized. To tackle multi-scale issues, a multiresolution strategy is employed on the friction parameter, thus allowing to initialize the optimization with a coarse friction resolution and refining it iteratively throughout the training for regularization purposes.
To illustrate the efficiency of the method and its sensitivity to the friction parameter dimension, two river hydraulic modeling test cases will be discussed. Overall, the proposed method appears efficient and robust. Moreover, it is simple to implement (non-intrusive) compared to more traditional Variational Data Assimilation approaches making it a viable strategy to further enhance for rapid flood forecasts.

Julien Demange-Chryst - ONERA, IMT - Mardi 18/06 à 15h10
Variational autoencoder with weighted samples for high-dimensional non-parametric adaptive importance sampling

Adaptive importance sampling is a well-known family of algorithms for density approximation, generation and Monte Carlo integration including rare event estimation. The main common denominator of this family of algorithms is to perform density estimation with weighted samples at each iteration. However, the classical existing methods to do so, such as kernel smoothing or approximation by a Gaussian distribution, suffer from the curse of dimensionality and/or a lack of flexibility. Both are limitations in high dimension and when we do not have any prior knowledge on the form of the target distribution, such as its number of modes. Variational autoencoders are probabilistic tools able to represent with fidelity high-dimensional data in a lower dimensional space. They constitute a parametric family of distributions robust faced to the dimension and since they are based on deep neural networks, they are flexible enough to be considered as non-parametric models. In this communication, we propose to use a variational autoencoder as the auxiliary importance sampling distribution by extending the existing framework to weighted samples. We integrate the proposed procedure in existing adaptive importance sampling algorithms and we illustrate its practical interest on diverse examples.

Armand Foucault- IMT, Université Paul Sabatier - Mardi 18/06 à 14h45
A general approximation lower bound in Lp norm, with applications to feed-forward neural networks

We study the fundamental limits to the expressive power of neural networks. Given two sets F, G of real-valued functions, we first prove a general lower bound on how well functions in F can be approximated in Lp(μ) norm by functions in G, for any p≥1 and any probability measure μ. The lower bound depends on the packing number of F, the range of F, and the fat-shattering dimension of G. We then instantiate this bound to the case where G corresponds to a piecewise-polynomial feed-forward neural network, and describe in details the application to two sets F: Hölder balls and multivariate monotonic functions. Beside matching (known or new) upper bounds up to log factors, our lower bounds shed some light on the similarities or differences between approximation in Lp norm or in sup norm, solving an open question by DeVore et al. (2021). Our proof strategy differs from the sup norm case and uses a key probability result of Mendelson (2002).

Lilit Hovsepyan - INRAE, Université Le Mans - Mardi 18/06 à 13h25
One-Step estimation procedure in univariate and multivariate GLMs with categorical explanatory variables

Generalized linear models are commonly used for modeling relationships in both univariate and multivariate contexts, with parameters traditionally estimated via the maximum likelihood estimator (MLE). MLE, while efficient, often requires a Newton-Raphson type algorithm for computation, making it time-intensive particularly with large datasets or numerous variables. Although faster, alternative closed form estimators lack the efficiency. In this topic, we propose a fast and asymptotically efficient estimation of the parameters of generalized linear models with categorical explanatory variables. It is based on a one-step procedure where a single step of the gradient descent is performed on the log-likelihood function initialized from the explicit estimators. This work presents the theoretical results obtained, the simulations carried out and an application to car insurance pricing.
Multivariate GLMs are studied in many scientific contexts. In insurance sector actuaries and risk managers precisely, they allow to assess the joint probabilities of various events occurring simultaneously, such as multiple claims or correlated risks across different insurance policy types (e.g., life, property, and auto). Copula models provide flexible tools to model multivariate variables by distinguish marginal effects from the dependence structure. In this setting, the copula parameter which quantify the (non-linear) dependency of the coordinates and the parameters of the marginal distributions are unknown and have to be estimated jointly.
In order to infer the parameters, maximum likelihood estimators (MLE) can be used due to the asymptotic properties. However, MLE is generally not in closed-form expression and is consequently time consuming. An alternative procedure, called inference for margins estimators (IFM), has been proposed in (Xu 1996, Joe 1997, 2005). In the IFM procedure, parameters of the marginals are estimated separately and simultaneously and plug-in to obtain finally the copula parameter. Although, IFM-MLE can still be time-consuming for this reason in order to estimate the copula parameter, fast and asymptotically efficient OS-CFE are used to estimate the parameters of the marginals and plug-in to estimate the copula parameter with the IFM method.

Sophia Yazzourh - IMT, Université Paul Sabatier - Mardi 18/06 à 13h50
Bayesian Outcome Weighted Learning

L'un des objectifs principaux de la médecine de précision statistique est d'apprendre des règles de traitement individualisées optimales ou "Individualized Treatment Rules" (ITRs). La méthode "Outcome Weighted Learning" (OWL) propose pour la première fois, une approche basée sur la classification, ou l'apprentissage automatique, pour estimer les ITRs. Elle reformule le problème d'apprentissage des ITR optimales en un problème de classification pondérée, qui peut être résolu en utilisant des méthodes d'apprentissage automatique, telles que les machines à vecteurs de support. Dans cet article, nous introduisons une formulation bayésienne de l'OWL. En partant de la fonction objective de l'OWL, nous générons une pseudo-vraisemblance qui peut être exprimée comme un mélange d'échelles de distributions normales. Un algorithme de Gibbs sampling est développé pour échantillonner la distribution postérieure des paramètres. En plus de fournir une stratégie pour apprendre une ITR optimale, l'OWL bayésien offre (1) une approche méthodique pour la génération de règles de décision apprises sur données dispersées et (2) une approche probabiliste naturelle pour estimer l'incertitude des recommandations de traitement ITR elles-mêmes. Nous démontrons la performance de notre méthode à travers plusieurs études de simulation.