Measure-theoretic Approaches and Optimal Transportation in Statistics
21-25 November 2022 - IHP, Paris
The Wasserstein distance in Optimal transportation has proved to be useful for a wide range of learning tasks such as generative models, domain adaptation or supervised embeddings. It is also an important metric for Topological Data Analysis and Geometric inference. More generally, distances on the space of probability measures, such as the maximum mean discrepancy, have shown to be powerful tools in statistical learning.
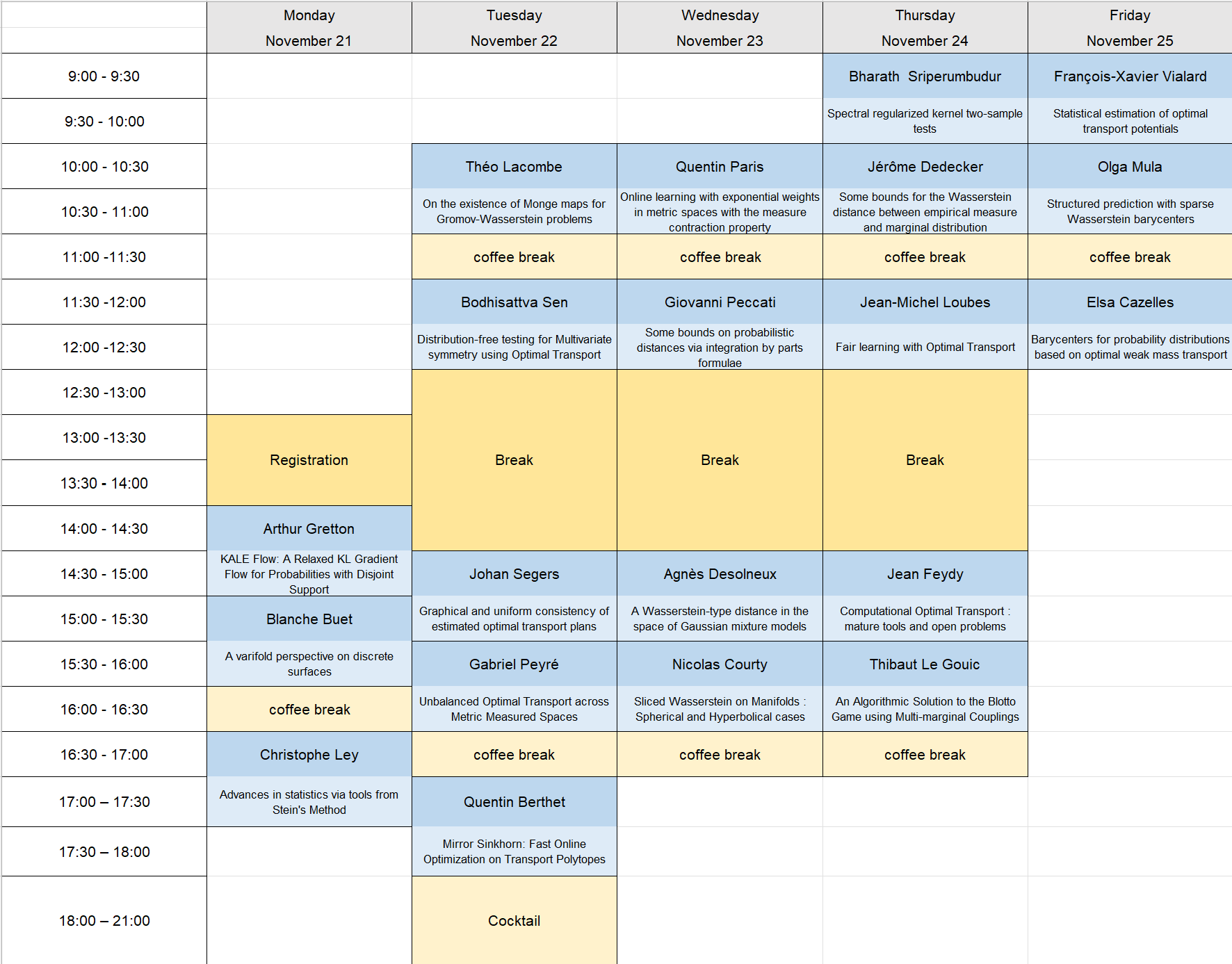
Program
Invited Speakers
- Quentin Berthet (Google Research)
- Blanche Buet (LMO, Orsay)
- Elsa Cazelles (IRIT, Toulouse)
- Nicolas Courty (IRISA, Rennes)
- Jérôme Dedecker (MAP5, Paris)
- Agnès Desolneux (Centre Borelli, Saclay)
- Jean Feydy (HeKA, INRIA Paris)
- Arthur Gretton (UCL, London)
- Théo Lacombe (LIGM, Champs sur Marne)
- Thibaut Le Gouic (IMM, Marseille)
- Christophe Ley (Université du Luxembourg)
- Jean-Michel Loubes (IMT, Toulouse)
- Olga Mula (CEREMADE, Dauphine)
- Axel Munk (Göttingen & Planck)
- Quentin Paris (HSE, Moscow)
- Giovanni Peccati (Luxemburg)
- Gabriel Peyré (DMA, ÉNS)
- Johan Segers (UC Louvain)
- Bodhisattva Sen (Columbia, New York)
- Bharath Kumar Sriperumbudur (Pennsylvania State University)
- François-Xavier Vialard (LIGM, Université Gustave Eiffel)
Application
Application for this event is currently open.
