Journée Algèbre Linéaire à Amiens
→
Europe/Paris
Sophie Germain (Amiens - UFR des Sciences)
Sophie Germain
Amiens - UFR des Sciences
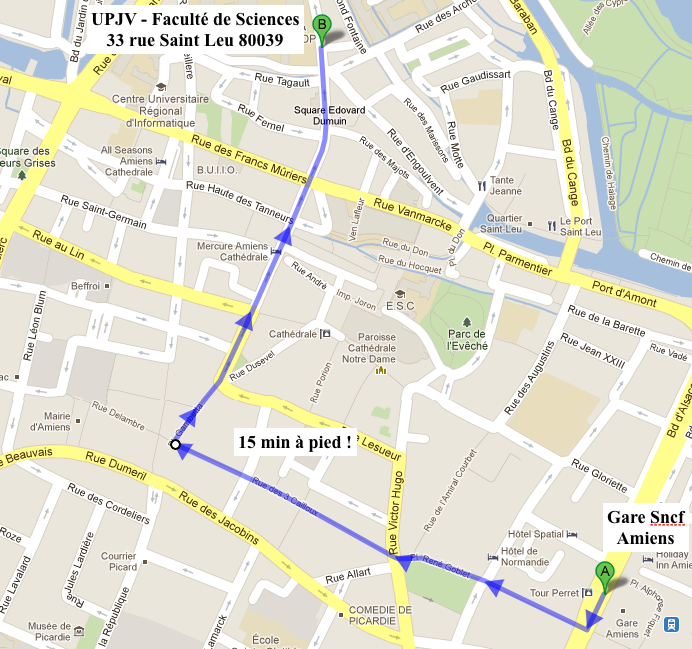
33, rue Saint-Leu, 80039 AMIENS
Description
Présentation de la journée
Cette journée a pour but de rassembler les acteurs mathématiques de la région Hauts-de-France autour de l'algèbre linéaire numérique et de ses applications.
Orateurs et oratrices
- Yousef Saad (Université du Minnesota)
- Marcos Raydan (Université Nova de Lisboa)
- Antoine Levitt (Université Paris-Saclay)
- Nicole Spillane (CNRS & École Polytechnique)
- Youcef Mammeri (Université Jean Monnet)
Inscriptions
Inscription gratuite mais obligatoire. Le nombre de participant⋅e⋅s est limité à 30 personnes.
Lieu de la journée
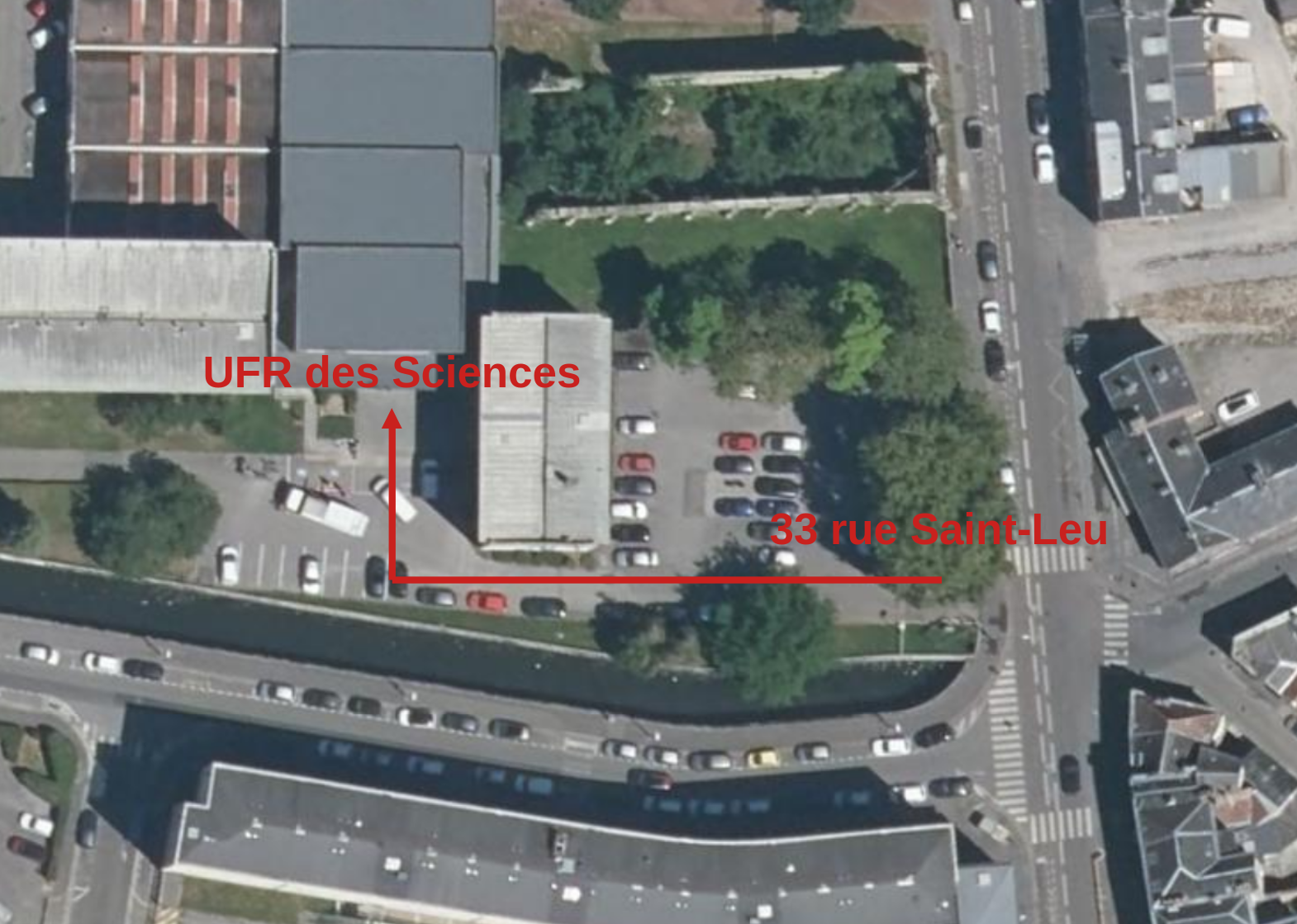
La journée se déroulera à l'UFR des Sciences, 33 rue Saint-Leu, 80039 Amiens, en salle Sophie Germain.
Vous trouverez un plan pour venir au 33 rue Saint-Leu depuis la gare ici.
Une fois sur place, l'UFR se trouve derrière le parking, et la salle Sophie Germain se situe au fond du hall d'entrée sur la droite.
Financements
Cette journée est financée par le LAMFA et l'Université de Picardie Jules Verne.

Organisateurs

