Modèle de la jonction de Josephson, systèmes dynamiques sur ${\mathbb T}^2$, surfaces déterminantales et les équations de Painlevé 3

par Alexey Glutsyuk (CNRS, UMPA, ENS de Lyon)

vendredi 10 janv. 2025, 10:30 → 11:30 Europe/Paris

207 (Bat 1R2)

L'effet de tunnel  prédit par B.Josephson (Prix Nobel 1973) concerne la   jonction de Josephson : un couple de supraconducteurs 
séparés par une couche de diélectrique très mince. Il consiste en l'existence d'un  supracourant qui la traverse et les  équations qui le gouvernent. La jonction de Josephson surchuntée est modélisée par une  famille d'équations différentielles sur le tore bidimensionnel, qui dépend de 3 paramètres:  l'abscisse $B$, l'ordonnée $A$ et la fréquence $\omega$. Nous étudions son nombre de rotation $\rho(B,A;\omega)$ comme fonction de $(B,A)$ à $\omega$ fixé. Les zones de verrouillage de phase sont ceux des ensembles de niveau $L_r:=\{\rho(B,A)=r\}\subset{\mathbb R}^2$ qui ont intérieurs non vides. Ils existent uniquement  pour les valeurs entières $r$ du nombre de  rotation : cet effet de quantisation a été découvert par V.M. Buchstaber, O.V. Karpov et S.I. Tertychnyi. Elles sont des analogues des célèbres langues d'Arnold. Chaque $L_r$ est une chaine infinie de  domaines allant  verticalement à l'infini et séparés par des points nommés constrictions (sauf pour ceux où $A=0$).  Voir les portraits des zones de verrouillage  ci-dessous pour $\omega=2, 1,  0.3$.

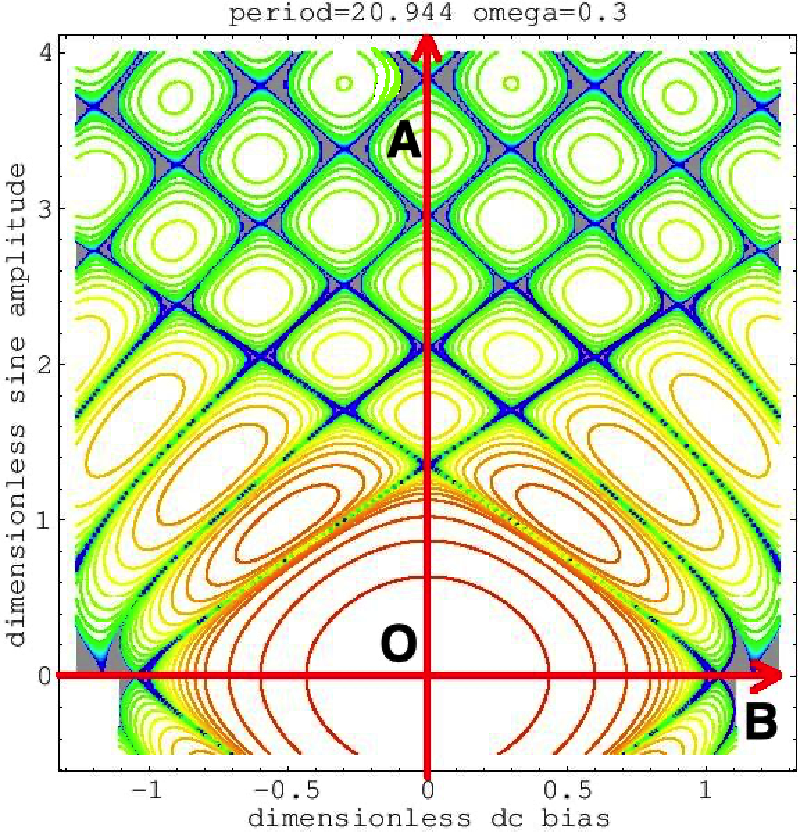
Avec Yulia Bibilo, nous avons montré, que toutes les constrictions dans $L_r$ sont sur la droite verticale $\Lambda_r:=\{ B=\omega r\}$.

Buchstaber, Karpov et Tertychnyi ont découvert une description équivalente du modèle par systèmes linéaires d'équations différentielles sur ${\mathbb C}$.  Buchstaber et  Tertychnyi ont montré, qu'ils sont équivalents aux équations de Heun doublement confluentes spéciales.  Ils ont décrit les ensembles de paramètres d'équation de Heun ayant des solutions polynomiales: les courbes déterminantales. 

Nous présentons une extension 4-dimensionelle du modèle dont l'espace de paramètres est feuilleté par des familles isomonodromiques   gouvernées par Painlevé 3. En utilisant des résultats sur les surfaces déterminantales (les  feuille-saturées des courbes déterminantales), 
nous démontrons la formule pour les genres de ces courbes (la conjecture de Netay et notre résultat en commun). Nous présenterons un survol de résultats et  de questions ouvertes.