Name: Yair Glasner: "Boomerang subgroups and the Nevo-Stuck-Zimmer theorem"
Start: 2022-09-28T14:00:00+02:00
End: 2022-09-28T15:00:00+02:00
Location: UMPA

Description

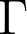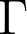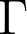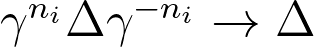Let $\Gamma$ be a countable group and $\mathrm{Sub}(\Gamma)$ its Chabauty space, namely the compact $\Gamma$ -space of all subgroups of $\Gamma$ . We call a subgroup $\Delta \in \mathrm{Sub}(\Gamma)$ a boomerang subgroup if for every $\gamma \in \Gamma$ , $\gamma^{n_i} \Delta \gamma^{-n_i} \rightarrow \Delta$ for some subsequence 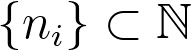$\{n_i \} \subset \mathbb{N}$ . 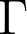Poincar\'{e} recurrence implies that $\mu$ -almost every subgroup of $\Gamma$ is a boomerang, with respect to every invariant random subgroup $\mu$ . I will discuss boomerang subgroups and in particular, I will prove that every boomerang subgroup in $\Gamma = \mathrm{SL}_n(\mathbb{Z}), \ n \ge 3$ is either finite and central or of finite index. This gives a simple new proof for the Nevo-Stuck-Zimmer theorem in this case. 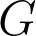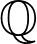More generally this method applies for lattices of the form $G(\mathbb{Z})$ where $G$ is a Chevaley group over $\mathbb{Q}$ .

This is a joint work with Waltraud Lederle.

Yair Glasner: "Boomerang subgroups and the Nevo-Stuck-Zimmer theorem"

435

UMPA