HyPNuT : Hyperbolic Problems - Numerics and Theory

Nov 5, 2025, 12:00 PM → Nov 7, 2025, 2:45 PM Europe/Paris

Amiens

This workshop will bring together researchers working on both the theoretical and numerical aspects of hyperbolic partial differential equations. Its main goal is to promote the exchange and dissemination of the latest developments within the hyperbolic PDE community.

A key objective is to foster dialogue between the theoretical and numerical communities, with the hope that this interaction will spark new ideas and lead to future collaborations.

The workshop will take place within UFR des Sciences, 33 rue Saint-Leu, Amiens, in room BC42. The following map shows how to go to room BC42 (4th floor) inside UFR des Sciences.

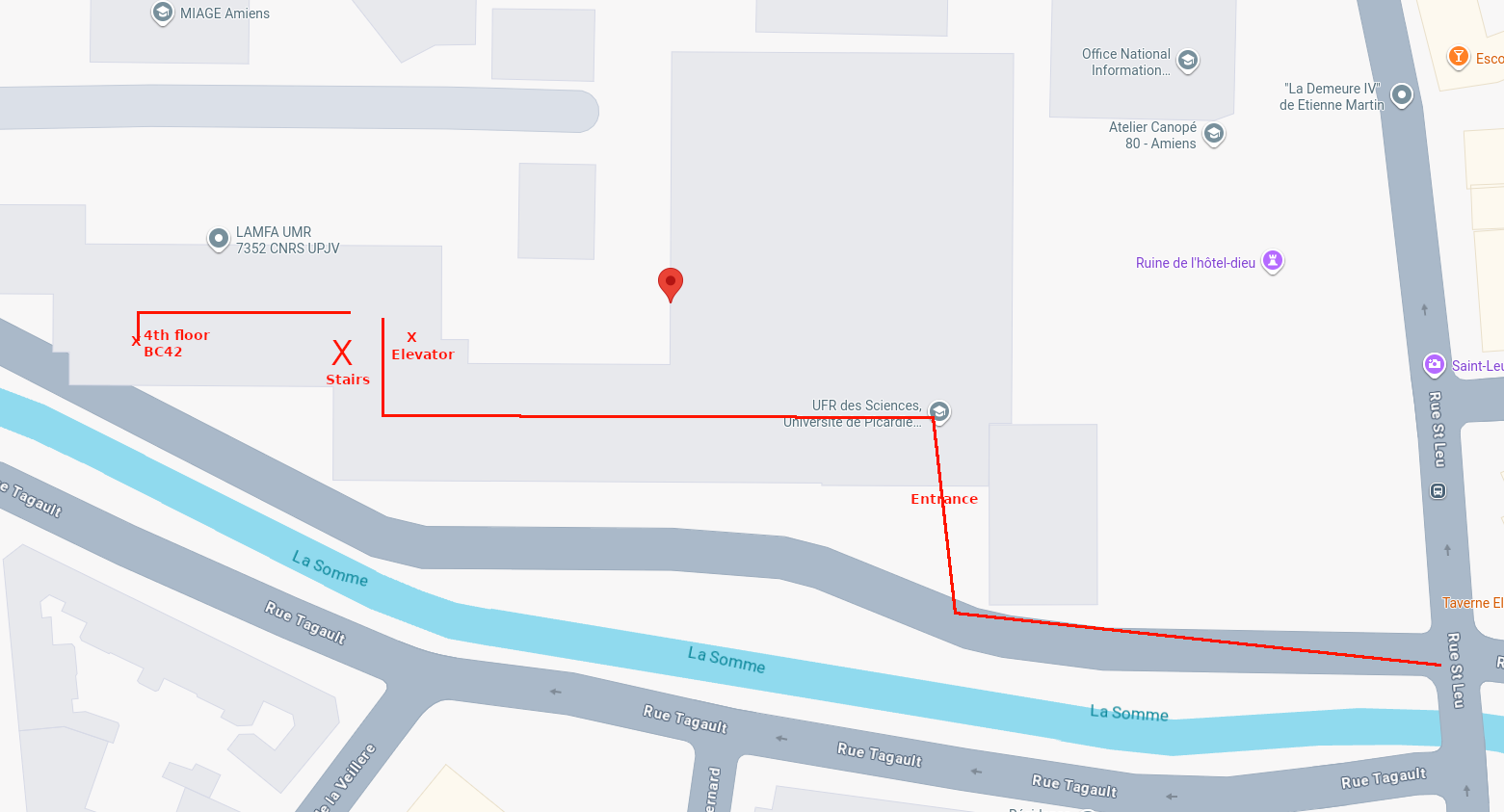
The meals will take place in the following places:

• Wednesday 05/11 lunch: Restaurant Universitaire Saint-Leu, rue Vanmarcke
• Wednesday 05/11 dinner, 7:30 PM: Brasserie Jules, 18 boulevard d'Alsace Lorraine
• Thursday 06/11 lunch: Restaurant Universitaire Saint-Leu, rue Vanmarcke
• Thursday 06/11 dinner, 7:30 PM: Brasserie de l'Horloge, 7 rue des Sergents
• Friday 07/11 lunch: L'Echanson, 21 rue Flatters

 

The Hotel is Appart'City Confort Amiens Gare, 80 boulevard d'Alsace Lorraine. It's about 500m from the train station and 1km from the conference place.

The following map shows all these meal places, as well as the train station, the conference place (UFR des Sciences) and the Appart'City hotel.

 

Wed, November 5

12:30 PM → 2:00 PM Lunch

Restaurant Universitaire Saint-Leu

2:30 PM → 3:15 PM Nonlocal macroscopic models of multi-population pedestrian flows for walking facilities optimization

We consider a class of nonlocal crowd dynamics models for N populations with different destinations trying to avoid each other in a confined walking domain.
This can be formalized in a initial-boundary value problem for a system of nonlocal conservation laws, where the velocity vector field of each population depends on a nonlocal operator depending on the current density distribution.
To account for the presence of obstacles, we proposed to evaluate the nonlocal operators on the convolution product of a kernel with the extended density including the presence of obstacles.
Under suitable regularity assumptions, we prove a well-posedness result for the corresponding weak entropy solutions.
The trick of incorporating the obstacles in the nonlocal operator allows to avoid including them in the vector field of preferred directions.
In particular, we can address shape optimization problems aiming at finding the optimal position of the obstacles to minimize the total travel time,
rewriting them as standard PDE-constrained optimization. In addition, to accelerate the numerical optimization procedure,
we propose to address the computational bottleneck represented by the convolution products by a Finite Difference scheme that couples high-order WENO approximations
for spatial discretization, a multi-step TVD method for temporal discretization, and a high-order numerical derivative formula to approximate the derivatives of nonlocal terms, and in this way avoid excessive calculations

Speaker: Paola Goatin (Inria Côte d'Azur)

3:15 PM → 4:00 PM Local fully discrete entropy stability for a second-order scheme for scalar hyperbolic equations

This talk concerns the numerical approximations of the weak solutions of scalar hyperbolic conservation laws. After showing how to bypass the barrier theorems for the linear advection, the derivation of a second-order entropy-stable scheme will be presented for non-linear equations. The fully discrete stability result will be established for regular strictly convex entropy and under a parabolic CFL-like condition. Some numerical experiments will be presented to assess the accuracy and the stability of the proposed scheme.

Speaker: Ludovic Martaud (Inria Rennes)

4:00 PM → 4:30 PM Coffee break

4:30 PM → 5:15 PM A two-speed relaxation system for Euler equations, and application to low Mach flows

We introduce a relaxation system to approximate the solutions to the barotropic Euler equations. We show that the solutions to this two-speed relaxation model can be understood as viscous approximations of the solutions to the barotropic Euler equations under appropriate sub-characteristic conditions. Our relaxation system is a generalization of the well-known Suliciu relaxation system, and it is entropy satisfying. A Godunov-type finite volume scheme based on the exact resolution of the Riemann problem associated with the relaxation system is deduced, as well as its stability properties. In a second part, we show how the new relaxation approach can be successfully applied to the numerical approximation of low Mach number flows. We prove that the underlying scheme satisfies the well-known asymptotic-preserving property in the sense that it is uniformly (first-order) accurate with respect to the Mach number, and at the same time it satisfies a fully discrete entropy inequality. This discrete entropy inequality allows us to prove strong stability properties in the low Mach regime. At last, numerical experiments are given to illustrate the behaviour of our scheme.

Speaker: Francois Bouchut (CNRS & Université Gustave Eiffel)

5:15 PM → 6:00 PM Thermodynamically coherent models for three-phase transition

We present in this talk a model for the transition between three possible phases of a same compressible fluid. To do this, we extend the usual formalism based on maximizing the specific entropy of the mixture to the three-phase case and study in particular the characterization of the triple point, which corresponds to the pressure and temperature values at which the three phases can coexist. We then deduce a (non-strictly) convex entropy at thermodynamic equilibrium. Focusing on the case of tin and its liquid, beta solid and gamma solid phases, we construct a complete equation of state and study a wide range of exact solutions to the associated Euler equations. This is a joint work with Hervé Jourdren and Corentin Stéphan.

Speaker: Nicolas Seguin (Inria)

7:30 PM → 9:30 PM Dinner

Thu, November 6

9:45 AM → 10:30 AM An entropy-dissipative quadrature-based closure for moment systems

The method of moments is commonly used to reduce a kinetic equation into a fluid model. It can be seen as a semi-discretization with respect to the kinetic variable, and it results in a system of balance laws that needs additional closure relations. The choices made in this construction have impacts on the properties of the resulting system, namely the strong or weak hyperbolicity, the entropy dissipation, or the geometry of the admissible solution set. Among the closures available in the literature, the quadrature-based ones provide a simple construction and good algorithmic properties. But the mathematical structure of the resulting system of PDE yields discrepancies compared to the original kinetic equation. I will present the common construction and properties of the quadrature-based closures, and provide an alternative based on symmetrization techniques to retreive strong hyperbolicity and a tuned entropy dissipation.

Speaker: Teddy Pichard (École Polytechnique)

10:30 AM → 11:00 AM Coffee break

11:00 AM → 11:45 AM Scalar Approach to ARZ-Type Systems of Conservation Laws

We are interested in 2 × 2 systems of conservation laws of special structure, including
generalized Aw-Rascle and Zhang (GARZ) models for road traffic. The simplest representative
is the Keytz-Kranzer system, where one equation is nonlinear and not coupled to the other, and
the second equation is a linear transport which coefficients depend on the solution of the firstequation.
In GARZ systems, the coupling is stronger, they do not have the “triangular” structure of
Keytz-Kranzer.

In our setting, we claim that it makes sense to address these systems via a kind of splitting approach.
Indeed, in 2008, Panov proposed a robust framework for solving linear transport equations with
divergence free coefficients. Our idea is to use this theory for the second equation of GARZ
systems, and to exploit discontinuous flux theory advances for the first equation of the
system.

Speaker: Abraham Sylla (LAMFA, UPJV)

11:45 AM → 12:30 PM Artificial numerical viscosity to get discrete entropy inequalities

When considering the numerical approximation of weak solutions of systems of conservation laws with source term, the satisfaction of discrete entropy inequalities is, in general, very difficult to be obtained. In the present talk, we present a suitable control of the artificial numerical viscosity in order to recover the expected discrete entropy inequalities. Moreover, the artificial viscosity control turns out to be very easy and it can be applied to any first-order finite volume scheme in a very convenient way.

Speaker: Christophe Berthon (Universtité de Nantes)

12:45 PM → 2:00 PM Lunch

2:30 PM → 3:15 PM "Sur le modèle de Hughes en une dimension" / "On the one-dimensional Hughes' model"

Le modèle pour évacuation piétonnière proposé par R.L. Hughes au début des années 2000 combine l'évacuation des agents en suivant la dynamique d'une loi de conservation avec champ de vitesses discontinu et l'ajustement instantané dudit champ pénalisant les régions à haute densité d'agents. L'analyse mathématique de cet élégant modèle reste délicate, à cause des singularités de chacune des équations.
Deux aspects de la théorie d'existence des solutions seront présentés : l'approximation par un système de particules déterministe ("Follow-the-Leader") et l'approche par point fixe. Les deux sont limités au cas académique des "coûts affines". La première est constructive, basée sur un modèle microscopique qui a un intérêt propre. La seconde apparaît plus flexible car elle s'adapte facilement à des variantes du modèle original.
Le cas 2D sera brièvement discuté.
L'exposé est basé sur les travaux menés avec M.D. Rosini, G. Stivaletta et T. Girard.
/
The pedestrian evacuation model proposed by R.L. Hughes in early 2000s combines agents' evacuation governed by a conservation law with discontinuous velocity field and instantaneous adjustment of the velocity field penalizing high-density regions. The mathematical analysis of this elegant model remains delicate, due to the singularities of both PDEs.
Two aspects of the existence theory will be presented: the deterministic many-particle ("Follow-the-Leader") approximation and the fixed-point approach. Both approaches are restricted to the academic case of ``affine costs''. The first one is constructive, based upon a miscroscopic model of interest on its own. The second approach appears more flexible, it adapts to several variants of the original model.
The 2D case will be briefly discussed.
The talk is based upon collaborations with M.D. Rosini, G. Stivaletta and T. Girard.

Speaker: Boris Andreianov (Université de Tours)

3:15 PM → 4:00 PM Mathematical Modeling of One-Way Pressure-Activated Valves for Gas

Our goal is to introduce a mathematical model for gas flow through a one-way valve which opens and closes (any value between fully open and fully closed is attainable) depending on the gap between the upstream and the downstream values of the pressure. This can be done by representing the valve as a unilateral point constraint on the gas flow, and introducing a suitable non-classical Riemann Solver which dictates the local behavior of the solution at the valve location.

We are particularly interested in the possibility to avoid chattering (the fast switch on and off of the valve), which, from a purely mathematical point of view, means that we want the non-classical Riemann Solver to be coherent.

This talk, based on an ongoing collaboration with Alice Gauthier, Ulrich Razafison and Massimiliano D. Rosini, will provide an overview of the theoretical and numerical results we obtained to this day and some perspective directions of investigation.

Speaker: Carlotta Donadello (Université Marie et Louis Pasteur)

4:00 PM → 4:30 PM Coffee break

4:30 PM → 5:15 PM The Morawetz problem for supersonic flow with cavitation

We are concerned with the existence and compactness of entropy solutions of the compressible Euler system for two dimensional steady potential flow around an obstacle for a polytropic gas with supersonic far-field velocity. This problem was first formulated by Morawetz in 1985 and has remained open since then. In this paper, we develop a complete compactness framework that allows for cavitation and show how it can be applied to obtain an existence theorem for the Morawetz problem by developing a new entropy analysis, in combination with a vanishing viscosity method and compensated compactness ideas. The main difficulty is that the problem becomes singular as the flow approaches cavitation, resulting in a loss of strict hyperbolicity and a singularity of the entropy equation for the case of adiabatic exponent 𝛾=3. Our analysis provides a complete description of the entropy and entropy-flux pairs via the Loewner-Morawetz relations, which leads to the establishment of the compensated compactness framework. As direct applications of our entropy analysis and the compensated compactness framework, we further obtain the compactness of entropy solutions and the weak continuity of the compressible Euler system in the supersonic regime.

Speaker: Simon Schulz (Université de Versailles Saint-Quentin)

7:30 PM → 9:30 PM Dinner

Fri, November 7

9:00 AM → 9:45 AM Vacuum free boundary problems in ideal compressible MHD

In this talk we first discuss the different plasma-vacuum interface problems of ideal Magneto-Hydrodynamics for incompressible or compressible fluids. Then we focus on the plasma-vacuum interface problem for ideal relativistic Magneto-Hydrodynamics (RMHD) in three-dimensional Minkowski spacetime. The plasma flow is governed by the two-dimensional RMHD equations, while the vacuum magnetic and electric fields satisfy the Maxwell's equations. The plasma and vacuum magnetic fields are tangential to the interface; this renders a nonlinear hyperbolic free boundary problem with the boundary being non-uniformly characteristic. We prove the local-in-time existence and uniqueness of solutions for this nonlinear free boundary problem, provided that the plasma and vacuum magnetic fields do not vanish simultaneously at each point of the initial interface.
This is a joint work with Y. Trakhinin (Novosibirsk) and T. Wang (Wuhan).

Speaker: Paolo Secchi (Università degli Studi di Brescia)

9:45 AM → 10:30 AM Stability of discrete shock profiles for diffusive finite difference schemes of systems of conservation laws

This talk deals with the stability analysis of discrete shock profiles
for systems of conservation laws. These profiles correspond to
approximations of shocks of systems of conservation laws by
conservative finite difference schemes. Discontinuous solutions
appear naturally in the study of systems of conservation laws,
which can model many physical situations, such as gas dynamics.
Existence and stability of discrete shock profiles for each stable
shock of the approximated system of conservation laws is seen as an
improved consistency condition and implies that the finite difference
scheme should be able to approach discontinuities fairly precisely.

The aim of the talk is to review some stability results regarding
discrete shock profiles and to present a recent effort to extend them.
More precisely, most results known up until recently are focused on the
stability of discrete shock profiles associated with shocks of small
amplitude. The talk will focus on a nonlinear orbital stability result
for discrete shock profiles in quite a general setting, where the
smallness assumption on the shock's amplitude is replaced by a spectral
stability assumption on the linear operator obtained by linearizing the
numerical scheme about the discrete shock profile. This nonlinear
orbital stability result relies on a precise description of the Green's
function of the linearization about discrete profiles.

Speaker: Lucas Coeuret (Université de Lorraine)

10:30 AM → 10:45 AM Coffee break

10:45 AM → 11:30 AM A non-conservative scheme for hyperelastic materials circumventing the involution constraint

This study focuses on the development of numerical schemes for a monolithic hyperbolic Eulerian model that combines fluid and hyper-elastic solid dynamics. Solid behavior requires an additional equation for deformation, and traditional approaches represent this model variable using the gradient of the backward characteristics rather than the characteristics themselves. While this ensures a conservative formulation and facilitates the accurate capture of discontinuities, it necessitates solving a larger system of equations, four equations in 2D instead of two, and nine in 3D instead of three. Furthermore, preserving the irrotational property of the integrated gradients introduces additional complexity. To address these challenges, we propose directly integrating the transport equation for the backward characteristics, leading to a non-conservative formulation. To ensure that the integration remains consistent with the weak solutions of the model, we explore a simplified approach based on the Jin-Xin relaxation method. The proposed strategy will be assessed against traditional conservative methods to evaluate its consistency, effectiveness and computational efficiency.

Speaker: Alessia Del Grosso (Inria Bordeaux)

11:30 AM → 12:15 PM Numerical exploration of the Kreiss-Lopatinskii condition for finite difference schemes

The approximate resolution of hyperbolic problems using finite difference methods requires a specific treatment of boundary conditions: artificial truncation of the computational domain, incorporation of physical boundary conditions, and so on. Even if the interior scheme has good convergence properties, the choice of boundary scheme can seriously impair the quality of the overall approximation. I will introduce the key concepts involved in formulating the Kreiss–Lopatinskii condition, which characterizes the stability of the scheme, and present numerical tools for its concrete verification, developed in a work with N. Seguin and P. Le Barbenchon.

Speaker: Dr Benjamin Boutin (Université de Rennes 1)

12:30 PM → 2:30 PM Lunch