Cusps of caustics by reflection in a convex billiard table
par
salle 207 bâtiment 1R2
Institut de Mathématiques de Toulouse
Place a point light source inside a smooth convex billiard table (or mirror). The n-th caustic by reflection is the envelope of light rays after n reflections. Theorem: each of these caustics, for a generic point light source, has at least 4 cusps. Conjecture: there are exactly 4 cusps iff the table is an ellipse. Here are the 2nd, 5th and 8th caustics by reflection in an ellipse, each with 4 cusps (marked by gray disks; the light source is the white disk)
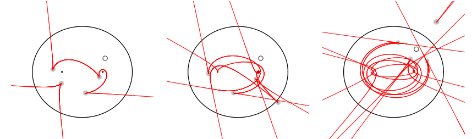
This is a billiard version of "Jacobi’s Last Geometric Statement", concerning the number of cusps of the conjugate locus of a point on a convex surface, proved so far only in the n=1 case. I will show various proofs, using curve shortening flow and Legendrian knot theory. (Joint work with Serge Tabachnikov, from Penn State, USA).
