Cubiques de genre 2 et autres incongruités tropicales.
par
(Travail en commun avec Erwan Brugallé et Lucía López de Medrano)
Il y a plusieurs façons d'obtenir des variétés tropicales. Par exemple comme limites d'images logarithmiques (par $\log_t$ appliqué au module de chaque coordonnées) de familles (de paramètre $t$) de sous-variétés algébriques du tore $(\mathbb{C}^\times)^n$.
Les images peuvent conserver des caractéristiques des objets algébriques, suffisamment, dans certains cas, pour obtenir des résultats intéressants sur les variétés algébriques originales.
On peut aussi définir les variétés tropicales, et certains de leurs invariants combinatoirement.
Dans le cas des hypersurfaces, les propriétés des objets tropicaux (combinatoires) reflètent bien celles des objets algébriques. Dans le cas des courbes, le genre $g$ et le degré $d$ peuvent être définis de manière combinatoire. Les courbes tropicales en dimension $2$ vérifient l'inégalité $$g \le \dfrac{(d-1)(d-2)}{2}$$ à l'image de leurs correspondantes complexes. Quand la dimension ambiante est supérieure, l'inégalité demeure côté algébrique mais nous avons montré quelle était fausse pour les courbes tropicales (combinatoires).
On peut ainsi avoir une courbe cubique tropicale de genre $2$ en dimension $3$...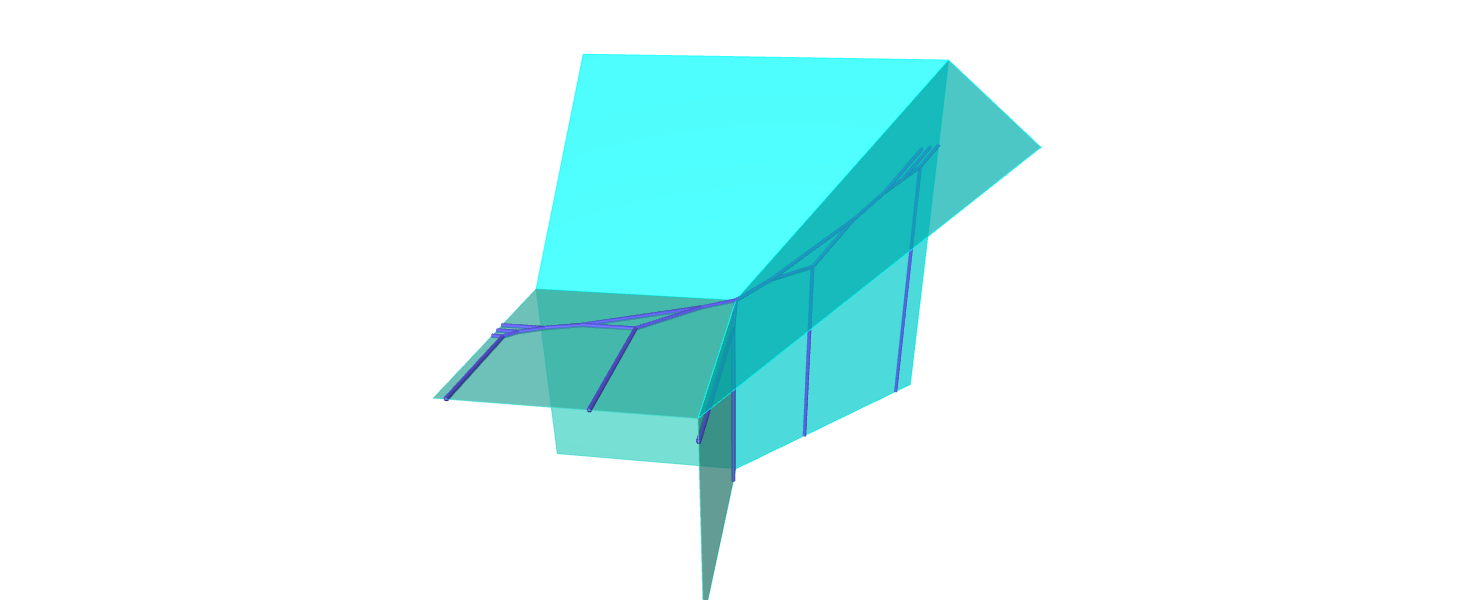
L'exposé devrait être élémentaire.