Name: Emmanuel Jacob, "La phase sous-critique en percolation continue en présence de longues arêtes."
Start: 2024-11-18T15:00:00+01:00
End: 2024-11-18T15:30:00+01:00
Location: No location set

Description

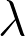Le modèle booléen est un graphe aléatoire dont les sommets sont donnés par un processus de points de Poisson d'intensité $\lambda>0$ sur $\mathbb R^d$ , et où deux sommets sont reliés par une arête si leur distance est inférieure à 1. Ce modèle exhibe une transition de phase "nette": pour $\lambda$ en-dessous d'un seuil critique $\lambda_c>0$ , le graphe n'a pas de composante connexe infinie, les composantes finies ne permettent typiquement pas de traverser un grand anneau, et la plus grande composante dans une boîte finie a une taille logarithmique.

Nous présentons un modèle plus général, où notamment une arête peut relier deux sommets arbitrairement éloignés. Nous étudions quand les grands anneaux sont typiquement traversés, et observons que contrairement au cas classique, ils peuvent être traversés pour 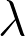$\lambda$ arbitrairement petit sans qu'il y ait pour autant de composante infinie.

L'argumentation est élémentaire et repose sur une inégalité de renormalisation satisfaite par ces modèles en l'absence de trop longues arêtes.